1700534488
1700534489
根据式(3.19)可计算出4个分支结点的信息熵为
1700534490
1700534491


1700534492
,
1700534493
1700534494


1700534495
,
1700534496
1700534497


1700534498
,
1700534499
1700534500


1700534501
1700534502
1700534503
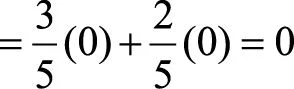
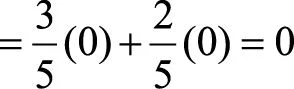
1700534504
.
1700534505
1700534506
于是,根据式(3.20)可计算出各个特征的信息增益为
1700534507
1700534508


1700534509
1700534510
1700534511


1700534512
.
1700534513
1700534514
显然,特征“写代码”的信息增益最大,所有的样本根据此特征,可以直接被分到叶结点(即见或不见)中,完成决策树生长。当然,在实际应用中,决策树往往不能通过一个特征就完成构建,需要在经验熵非0的类别中继续生长。
1700534515
1700534516
■ C4.5——最大信息增益比
1700534517
1700534518
特征A对于数据集D的信息增益比定义为
1700534519
1700534520


1700534521
,
1700534522
1700534523
(3.21)
1700534524
1700534525
其中
1700534526
1700534527


1700534528
,
1700534529
1700534530
(3.22)
1700534531
1700534532
称为数据集D关于A的取值熵。针对上述问题,我们可以根据式(3.22)求出数据集关于每个特征的取值熵为
1700534533
1700534534


1700534535
,
1700534536
1700534537

