1700534535
,
1700534536
1700534537


1700534538
,
1700534539
1700534540


1700534541
,
1700534542
1700534543
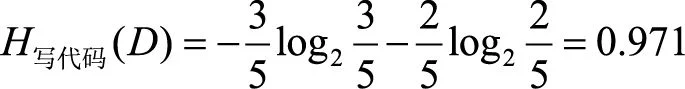
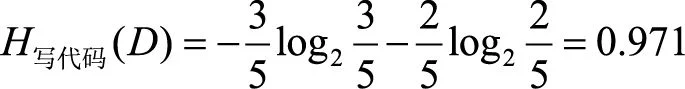
1700534544
.
1700534545
1700534546
于是,根据式(3.21)可计算出各个特征的信息增益比为
1700534547
1700534548


1700534549
1700534550
1700534551
信息增益比最大的仍是特征“写代码”,但通过信息增益比,特征“年龄”对应的指标上升了,而特征“长相”和特征“工资”却有所下降。
1700534552
1700534553
■ CART——最大基尼指数(Gini)
1700534554
1700534555
Gini描述的是数据的纯度,与信息熵含义类似。
1700534556
1700534557


1700534558
1700534559
1700534560
(3.23)
1700534561
1700534562
CART在每一次迭代中选择基尼指数最小的特征及其对应的切分点进行分类。但与ID3、C4.5不同的是,CART是一颗二叉树,采用二元切割法,每一步将数据按特征A的取值切成两份,分别进入左右子树。特征A的Gini指数定义为
1700534563
1700534564


1700534565
1700534566
1700534567
(3.24)
1700534568
1700534569
还是考虑上述的例子,应用CART分类准则,根据式(3.24)可计算出各个特征的Gini指数为
1700534570
1700534571
Gini(D|年龄=老)=0.4, Gini(D|年龄=年轻)=0.4,
1700534572
1700534573
Gini(D|长相=帅)=0.4, Gini(D|长相=丑)=0.4,
1700534574
1700534575
Gini(D|写代码=会)=0, Gini(D|写代码=不会)=0,
1700534576
1700534577
Gini(D|工资=高)=0.47, Gini(D|工资=中等)=0.3,
1700534578
1700534579
Gini(D|工资=低)=0.4.
1700534580
1700534581
在“年龄”“长相”“工资”“写代码”四个特征中,我们可以很快地发现特征“写代码”的Gini指数最小为0,因此选择特征“写代码”作为最优特征,“写代码=会”为最优切分点。按照这种切分,从根结点会直接产生两个叶结点,基尼指数降为0,完成决策树生长。
1700534582
1700534583
通过对比三种决策树的构造准则,以及在同一例子上的不同表现,我们不难总结三者之间的差异。
1700534584