1700535401


1700535402
图5.5是一个θ为一维的例子,其中棕色的曲线代表我们待优化的函数,记为f(θ),优化过程即为找到使得f(θ)取值最大的θ。在当前θ的取值下(即图中绿色的位置),可以计算,此时不等式右侧的函数(记为r(x|θ))给出了优化函数的一个下界,如图中蓝色曲线所示,其中在θ处两条曲线的取值时相等的。接下来找到使得r(x|θ)最大化的参数θ′,即图中红色的位置,此时f(θ′)的取值比f(θ)(绿色的位置处)有所提升。可以证明,f(θ′)≥r(x|θ)=f(θ),因此函数是单调的,而且从而函数是有界的。根据函数单调有界必收敛的性质,EM算法的收敛性得证。但是EM算法只保证收敛到局部最优解。当函数为非凸时,以图5.5为例,如果初始化在左边的区域时,则无法找到右侧的高点。
1700535403
1700535404


1700535405
1700535406
1700535407
图5.5 K均值算法的收敛性
1700535408
1700535409
由上面的推导,EM算法框架可以总结如下,由以下两个步骤交替进行直到收敛。
1700535410
1700535411
(1)E步骤:计算隐变量的期望
1700535412
1700535413


1700535414
.
1700535415
1700535416
(5.8)
1700535417
1700535418
(2)M步骤:最大化
1700535419
1700535420
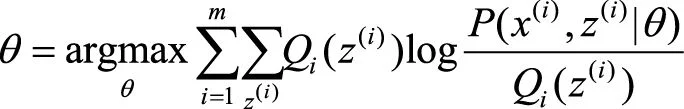
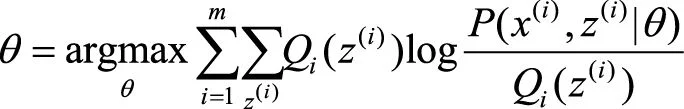
1700535421
.
1700535422
1700535423
(5.9)
1700535424
1700535425
剩下的事情就是说明K均值算法与EM算法的关系了。K均值算法等价于用EM算法求解以下含隐变量的最大似然问题:
1700535426
1700535427


1700535428
1700535429
1700535430
(5.10)
1700535431
1700535432


1700535433


1700535434
其中是模型的隐变量。直观地理解,就是当样本x离第k个簇的中心点μk距离最近时,概率正比于,否则为0。
1700535435
1700535436
在E步骤,计算
1700535437
1700535438


1700535439
1700535440
1700535441
(5.11)
1700535442
1700535443
这等同于在K均值算法中对于每一个点x(i)找到当前最近的簇z(i)。
1700535444
1700535445


1700535446
在M步骤,找到最优的参数,使得似然函数最大:
1700535447
1700535448


1700535449
.
1700535450