1700923499
1700923500
QED是解释带电粒子——如电子——如何相互作用,以及它们如何与光子相互作用的理论。单靠它就能解释除引力和原子核以外的所有自然现象。稍后我们将把注意力转向原子核内的现象,并解释为何原子核能保持稳定;它由一堆带正电的质子和不带电的中子构成,如果没有亚原子核现象,后者会在电排斥作用下瞬间飞散。几乎所有的东西,当然包括你看到的和感知的所有东西,都可以通过QED在最深的层次上被解释。物质、光、电和磁,这些都是QED[207]。
1700923501
1700923502
我们先来探索一个在本书中已经反复出现的系统:一个包含单个电子的世界。图4.2“小钟跃动”图上的小圆圈表示电子在某一时刻的可能位置。要推导在以后的某一时刻,在某位置X找到它的可能性,我们的量子规则说,要让电子从每个可能的起点跃至X。每次跳跃都会传递一块钟到X;将这些钟相加,就完成了。
1700923503
1700923504
我们下面要做的事情,一开始可能看似有点过度复杂,但当然是有价值的。这将会涉及到一些A、B和T——换言之,我们又要进入花呢外套和粉笔灰的领域了,但不会逗留太久。
1700923505
1700923506
如果一个粒子于零时刻从位置A出发并于T时刻到达位置B,我们就可以通过A到B的距离以及时间间隔T,计算出从A出发的钟需要逆时针旋转的圈数,并得到B处的钟。简而言之,我们可以把B处的钟写成C(A,O) P(A,B,T),其中C(A,0)表示A处在零时刻的初始钟,而P(A,B,T)体现出从A跃至B的旋转和收缩规则[208]。我们把P(A,B,T)称为从A到B的“传播子”(propagator)。一旦知道了从A到B的传播规则,我们就完成了准备,可以算出在X处找到粒子的概率。对于图4.2中的例子,我们有很多起始位置,所以就得把每个位置上的钟都传播到X,并把结果加起来。在我们看似牛刀杀鸡的记号中,最后的钟是:
1700923507
1700923508
C(X,T)=C(X,0) P(X1,X,T)+C(X2,0) P(X2,X,T)+C(X3,0) P(X3,X,T)+…
1700923509
1700923510
其中X1、X2、X3等标记了粒子在零时刻的所有位置(即图4.2中的小圆圈)。再说清楚一点,C(X3,0) P(X3,X,T)就是说“把零时刻位于X3的钟在T时刻传播到X”。不要被骗了,以为会发生什么取巧的事情。我们所做的,只是把已知的东西用一种花哨的方法简记下来:“考虑零时刻位于X3的钟,算出当粒子从X3出发并在T时刻运动到X时,这块钟需要旋转和收缩的量;并且对所有其他零时刻的钟做相同的事情,最后再把它们用钟相加的法则加起来。”相信你一定会认同这句话有点拗口;而笔者的这种记法,让人生更容易了一点。
1700923511
1700923512
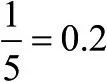
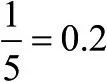
1700923513
我们当然可以把传播子看成是钟旋转和收缩规则的体现。但也可以把它看成是一块钟。为了澄清这条生硬的陈述,想象我们知道电子在T=0时能确定电子位于A处,并且它由一块大小为1、指向12点的钟所描述。可以用第二块钟来描述传播行为,其大小是原始钟需要收缩的量,而时刻为所需的旋转圈数。如果从A到B需要将原始钟缩小5倍,并转过2小时,则传播子P(A,B,T)可以用一个大小为、时刻为10点的钟来表示(即从12点方向往回转动2小时)。B处的钟就是通过将A处的原始钟“乘以”传播子的钟所得到的。
1700923514
1700923515
对了解复数的读者多提一句:正如每个C(X1,0)、C(X2,0)可以用复数表示,P(X1,X,T)、P(X2,X,T)也可以,并且前后两者的组合是根据两个复数相乘的数学法则进行的。对于不懂复数的读者这不要紧,因为用钟来描述也同样是准确的。前面两段只是为钟的旋转规则引入了一种稍微不同的思路:可以用另一块钟,来旋转和收缩已有的钟。
1700923516
1700923517
我们可以自由设计相乘的规则——即传播子,实现任何结果:将两块钟的大小相乘(1×0.2=0.2),并将两块钟的时间合并,使得第一块钟旋转的量等于12点减10点,这等于2小时。听起来笔者的确用上了屠龙之技,当只用考虑一个粒子时,这些显然没必要。但物理学者都很懒,一般他们不会大费周章,除非从长远来看能省时间。事实证明,当研究包含多个粒子——比如氢原子——的有趣情形时,这些小小的记号对于记录所有的旋转和收缩是非常有用的。
1700923518
1700923519
忽略掉细节,在我们计算宇宙某处找到单个粒子的概率时,只有两个关键因素。首先,需要指定钟的初始阵列,这包含了于零时刻在何处可能找到粒子的信息。其次,需要知道传播子P(A,B,T)它本身也是一块钟,包含了粒子从A跃至B的收缩和旋转规则。一旦知道了任意一对起止点的传播子是什么样子,我们就知道了所有的事情,便能很有信心地解出,一种穷极无聊的动力学所对应的宇宙仅包含单个粒子。但其实我们不该如此贬低这个结果,因为把粒子的相互作用加进游戏后,这种简单的状态并没有变复杂很多。所以现在就把相互作用加进来吧。
1700923520
1700923521


1700923522
1700923523
1700923524
图10.1:一对电子相互散射的一些方式。电子从左侧出发,在时刻T时,总是到达同一对位置X和Y处。这些图对应了粒子到达X和Y的不同方式。
1700923525
1700923526
图10.1形象地说明了所有我们要讨论的关键想法。这是我们第一次接触到费曼图(Feynman diagram),专业粒子物理学者的计算工具。我们的任务是,计算出在某个T时刻,在位置X和Y找到一对电子的概率。开始时,我们被告知电子在零时刻的位置;也就是说,我们被告知了电子的初始钟群是什么样子的。这很重要,因为能够回答这类问题,就等于知道了“在一个包含两个电子的宇宙中会发生些什么”。这听起来可能没什么大进展,但一旦弄清了这个问题,世界就是我们的囊中之物,因为我们会知道大自然的基本构件是如何相互作用的。
1700923527
1700923528
为了简化图像,我们只画出了一个空间维度。这完全不会影响结论。先来描述图10.1中一系列图的第一张。 T=0处的小点对应两个电子在零时刻可能的位置。为了方便说明,我们假设上方的电子可以位于三个位置其中之一,而下方的电子可以位于两个位置之一(在现实世界中,必须处理电子可以位于无穷个可能位置的情形,但如果要画出这种情形,会把墨用光的)。上方的电子在稍后某个时刻跃至A,并在那里做一些有趣的事情:它发射出一个光子(用波浪线表示)。这个光子之后跃至B,并在那里被另一个电子吸收。然后,上方电子由A跃至X,而下方电子由B跃至Y。这只是原来那对电子到达位置X和Y的无数种方式中的一种。我们可以把整个过程与一块钟关联起来——称之为“钟1”或者简称C1 。QED的工作就是,告诉我们游戏规则,让我们能推导出这块钟。
1700923529
1700923530
在进入细节之前,我们先来描绘出结果。最上方的图代表了最初的一对电子到达X和Y的万千种方式之一。其他的图代表了其他一些方式。这里的关键想法是,对于每一种电子到达X和Y的方式,我们都要确定出一块量子钟,而C1是一长列钟里的第一块[209]。钟尺寸(的平方)告诉我们,在X和Y找到一对电子的概率。因此,我们要再次想象,电子抵达X和Y不只有一条路径,而是通过所有可能的方式相互散射。如果看一下最后几张图,就会看到一些更繁复的电子散射方式。电子不仅交换光子,它们本身就能发射和再吸收光子;在最后两张图中,还发生了非常奇怪的事情。在这些图中,光子看似发射出电子,而电子“绕了一圈”又回到原点;我们稍后会就此展开讨论。目前,我们只需想象一系列愈发复杂的图,描述电子在最终到达X和Y之前如何发射和吸收了大量光子。我们需要想出各种各样让电子到达X和Y的方式,但有两条规则是非常明确的:电子可以从此处跃至彼处,发射或吸收一个光子。这就是全部的规则;电子可以跃动或者分枝。仔细观察就会发现,笔者画出的图中,没有一张违反这两条规则,因为它们从未涉及比两个电子和一个光子更复杂的结点。现在我们必须解释一下如何计算图10.1里每张图对应的钟。
1700923531
1700923532


1700923533
我们来把注意力集中在最上面一张图中,并说明如何确定与之关联的钟(C1)是什么样子。在过程开始时,有两个电子,它们每个都有一块钟。我们会根据钟的乘积法则,将它们相乘得到一块新的单块钟,用符号C表示。它们相乘是有意义的,因为钟实际上编码了概率;而如果有两个独立的概率,则要把它们合在一起就得乘起来。例如,掷两枚硬币,同时得到正面向上的概率是。同样,合并后的钟C告诉我们在两个电子的初始位置找到它们的概率。
1700923534
1700923535
剩下就是进行更多钟的乘法。上方电子跃至A,因此有一块钟与之关联;我们叫他P(1,A)(即“粒子1跃至A”)。同时,下方电子跃至B,这也有一块钟,称为P(2,B)。同样,还有两块钟,对应于电子跃至最终位置,把它们记作P(A,X)和P(B,Y)。最后,我们还有一块钟与光子关联,它从A跃至B。由于光子不是电子,光子的传播规则不一定与电子相同,因此我们应该用不同的符号表示它的钟。我们把光子跳跃对应的钟记作L(A,B)[210]。现在,我们简单把所有的钟乘起来,得到一块“主”钟:
1700923536
1700923537
R=C×P(1,A)×P(2,B)×P(A,X)×P(B,Y)×L(A,B)
1700923538
1700923539
现在我们已经非常接近完成了,还有额外的一些钟收缩需要算上,因为在电子发射或吸收光子时,QED的规则说,要引入一个收缩因子g。在我们的图中,上方的电子发射出光子,而下方电子吸收了它;这就引入了两个g因子,即g2。现在我们真的完成了,最终的“钟1”由C1=g2×R计算得到。
1700923540
1700923541
收缩系数g看似有些任意,但它的物理解释非常重要。它显然与电子发射光子的概率有关,而这就编码了电磁力的强度。我们得在计算中引入与现实世界的联系,因为我们计算的是真实的东西;就像牛顿引力常数G承载了引力强度的所有信息,g也承载了电磁力强度的所有信息[211]。
1700923542
1700923543
如果我们确实要完成一个完整的计算,现在就要把注意力转向第二张图;它代表了最初那对电子抵达相同目的地X和Y的另一种方式。第二张图和第一张十分相似,电子也从同一位置出发,但现在光子由上方电子在不同的空间位置和时刻发射出来,并被下方电子在不同的位置和时刻吸收。其余的事情和第一张图完全一样,这样我们就得到第二块钟“钟2”,用C2表示。
1700923544
1700923545
然后我们继续对每一个可能发射和吸收光子的地方都重复整个过程。还应该考虑到,电子可以从多种不同的可能位置出发。关键在于要考虑到每一种将电子送至X和Y的方式,而每种方式都对应一块钟。一旦我们集齐了所有的钟,就“只需”把它们加起来,产生一块最终的钟,其大小就能告诉我们在X处、Y处分别找到一个电子的概率了。这就完成了我们的任务,搞清楚了两个电子是如何相互作用的,因为我们能做的也只有计算出概率。
1700923546
1700923547
刚才所描述的确实就是QED的核心,而大自然中的其他相互作用也能从类似的方式中得到令人满意的描述[212]。笔者很快就会讲到这些,但现在还有其他几点发现要说明。
1700923548