1700947724
图2-10 重物作圆周运动,所以它的速度垂直于杆子
1700947725
1700947726
你们或许会对自己说,“喔!我得学习那个诀窍!”
1700947727
1700947728
不!这种诀窍仅对特殊类型的问题是有用的,在大多数情况下它是无效的。你们很少碰到恰巧要求绕固定点转动的某个物体的速度;没有规则说“速度垂直于杆子”或类似的东西。你们得尽可能经常使用常识。从几何学分析机械的一般概念在这里是很重要的——但不是任何特殊的规则。
1700947729
1700947730
现在我们知道了速度的方向。我们已经知道的速度的水平分量为1,因为它是滚轴速率的一半。但是你看!速度是直角三角形的斜边,该三角形与以杆子为斜边的直角形相似!求速度的数值并不比求它对其水平分量的比值更困难。我们可以从我们已经完全知道的其他三角形得到该比值(见图2-11)。
1700947731
1700947732


1700947733
1700947734
1700947735
图2-11 利用相似三角形求重物的速度
1700947736
1700947737
最后,关于动能,我们得到
1700947738
1700947739


1700947740
1700947741
1700947742
现在,谈谈符号的问题:动能肯定为正,由于我们测量的距离是对地面而言的,所以势能也为正,现在我所用的符号都完全正确。因而在任何时刻的能量为
1700947743
1700947744


1700947745
1700947746
1700947747
现在,为了用这种诀窍求力,我们需要对能量求微商,然后除以2,这样就一切都准备好了。“我用这种方法解这个问题表面上显得很容易,其实这是假象:我发誓,在我得到正确答案之前我做了不止一次。”
1700947748
1700947749
现在我们把能量对时间求微商。我不必为此事花太多的时间,我认为你们现在都已知道如何求微商,所以我们就直接给出dE /dt 的答案(顺便提及,它是所需力的2倍。)
1700947750
1700947751
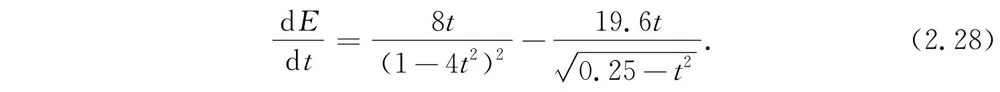
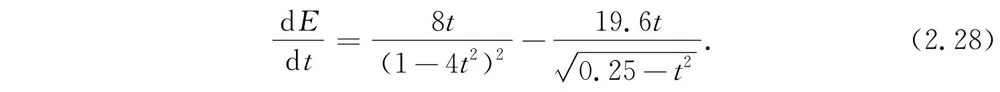
1700947752
1700947753
1700947754
这样,我就全部完成了:我只要把0.3代入t ,就完成了。不过,还没完——为得到正确的符号获得正确,我必须使用t =-0.3:
1700947755
1700947756


1700947757
1700947758
1700947759


1700947760
* 原文为 。——译者注
1700947761
1700947762


1700947763
现在我们来看看这结果是否有意义。如果没有运动,那我不必为动能操心,于是重物的总能量仅仅是它的势能,而它的微商应为重量产生的力[9] 。确实如此,这里所得结果与我们在第一章中计算的结果相同,都是 。
1700947764
1700947765
(2.29)式右边第一项为负,这是因为重物正在减速,所以它正在失去动能;第二项为正是由于重物正在上升,所以势能正在增加。无论如何,它们的符号彼此相反,这是我要知道的全部东西,而你们可以代入数值,果然,所得到的力与前面得到的相同:
1700947766
1700947767


1700947768
1700947769
1700947770
实际上,这就是我为什么一定要做这许多次的原因:在我第一次做这题后,对我的错误答案心满意足,我决定用另一种完全不同的办法试试。我用另一种办法做了以后,又满足于完全不同的答案!当你们辛苦地工作时,你们有时会想:“至少,我已经发现数学是前后矛盾的!”但是很快你们就发现了错误,正如我最后做的那样。
1700947771
1700947772
无论如何,这正是解这问题的两种方法。解任何具体问题不是只有唯一的一种方法。随着智力越来越强大,你们能够找到工作量少而又少的方法,但是这需要实践经验[10] 。
1700947773