1700947919
[10] 关于解这问题的另外三种方法,参见补充题解 ,从78页开始。
1700947920
1700947921
1700947922
1700947923
1700947924
费恩曼物理学讲义补编 [:1700946338]
1700947925
费恩曼物理学讲义补编 3 习题及解答复习课C
1700947926
1700947927
我们继续复习如何通过做一些习题来学习物理。我这里所选的习题都是精心设计的、复杂法的并且是困难的,我把容易些的习题留给你们自己去做。我也有所有教授都有的毛病——就是似乎永远不会有足够的时间,我想出了肯定比我们来得及做的更多的习题。因此我试图加快速度,为此,先把某些东西写在黑板上,并带着每位教授都有的错觉:如果他讲更多的东西,他就教给学生更多的东西。当然,人脑吸收材料的速率是有限的,然而我们还是会忽视这种现象。我们会不顾这些而讲得太快。所以,我想尽量讲得慢一点,并看看我们可以讲多少。
1700947928
1700947929
3-1 卫星运动
1700947930
1700947931
我们上次讲到的最后一个问题是卫星的运动。我们曾讨论这样的问题,若一个质点作垂直于太阳、行星或任何质量为M 的物体的半径的运动,它们的距离为a ,且具有在此距离处的逃逸速度,则该质点实际上是否能逃逸——因它不是不证自明的。如果质点是沿半径方向一直向外运动的,则它应该会逃逸 ;但如果它开始时沿垂直半径方向运动,那它是否逃逸是另一个问题(见图3-1)。
1700947932
1700947933


1700947934
1700947935
1700947936
图3-1 逃逸速度沿着半径指向和垂直于半径的情况
1700947937
1700947938
结果发现——如果我们还记得开普勒定律,再加上另外一些定律,如能量守恒定律——那么我们就能够算出要是质点不 逃逸,它会作椭圆运动,而且我们能算出它将达到多远的地方,这就是我们现在要做的事情。如果该椭圆的近日点是a ,那其远日点b 有多远?(顺便说说,我想把这问题写在黑板上,但是我发现我不会拼写近日点,见图3-2。)
1700947939
1700947940


1700947941
1700947942
1700947943
图3-2 椭圆轨道上人造卫星的近日点及远日点处的速度和距离
1700947944
1700947945
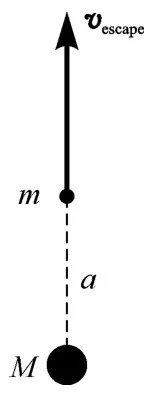
上次我们根据能量守恒算出了逃逸速度(见图3-3)。
1700947946
1700947947


1700947948
1700947949
1700947950

1700947951
1700947952
1700947953
图3-3 距离质量为M的物体a处的逃逸速度
1700947954
1700947955
现在,这是在半径a 处的逃逸速度公式。但是假定速度va 是任意的,而我们来求由va 表示的b 。能量守恒告诉我们,质点在近日点的动能和势能必定等于它在远日点的动能和势能——这样我们就能利用它来计算b ,一眼就看出:
1700947956
1700947957


1700947958
1700947959
1700947960
Infelizmente [1] ,我们却没有vb ,所以除非存在某种外部机制或者经分析而得出vb ,否则我们永远无法从(3.2)式求出b 。
1700947961
1700947962
但是如果我们记得开普勒的等面积定律,那么我们就知道,在给定的时间间隔内,在远日点扫过的面积和在近日点扫过的面积相等;在短时间间隔Δt 内,质点在近日点通过距离va Δt ,所以它扫过的面积约为a ·va Δt /2,而在远日点,质点经过的距离vb Δt ,扫过的面积约为bvb Δt /2,“面积相等”意指ava Δt /2等于bvb Δt /2——这意味着速度与半径反比地变化(见图3-4)。
1700947963
1700947964


1700947965
1700947966
1700947967


1700947968