1700948097
任何思维正常的人会说,火箭获得比速率u 更快的任何速率是不可能的。你们立刻就会明白,这种说法是不正确的。或许你们会说,那完全是显而易见的啊;很好,完全正确,但实际上它之所以正确是由于下面的原因。
1700948098
1700948099
让我们考察任意时刻的火箭,它可以以任意速率运动。如果我们跟随着火箭一同运动,并观察一段时间Δt ,我们看到什么呢?嗯,有一定质量Δm 的物质离开——它等于火箭的喷出率μ 乘时间Δt ,这些质量离开的速度为u (见图3-10)。
1700948100
1700948101


1700948102
1700948103
1700948104
图3-10 通过喷射出速度为u的质量Δm,火箭在Δt的时间间隔内增加了速度Δv
1700948105
1700948106
现在,这些质量向后抛出后,火箭向前运动增加多少呢?在它向前运动的速率必须满足总动量守恒。也就是说,它将以这样的方式获得一点速率Δv ,即如果火箭的壳体和剩余燃料在这瞬时的质量为m ,那么m 乘Δv 就应与这段时间向外抛射的动量,即Δm 乘u ,相等。这就是火箭理论的全部内容;基本火箭方程是:
1700948107
1700948108


1700948109
1700948110
1700948111
我们可以用μ Δt 代替Δm ,稍加推演,就可求出火箭达到给定速度要花多长 时间[4] ,但我们的问题是求出最后速度,而我们可以直接从(3.15)式来求:
1700948112
1700948113


1700948114
1700948115
1700948116
为了求出火箭从静止出发,最后达到的速度,你们对u (dm /m )从初始质量到最后质量求积分。现在u 假定为常数,所以可把它提到积分号外,因而我们得
1700948117
1700948118
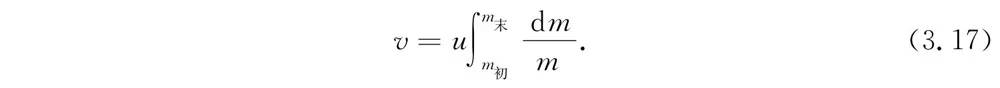
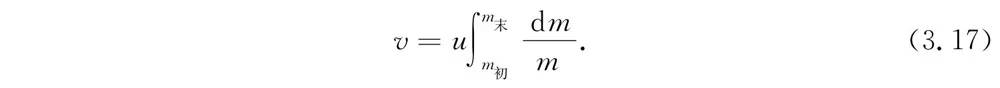
1700948119
1700948120
1700948121
dm /m 的积分,你们也许知道,也许不知道。让我们假定你们不知道。你们说,“1/m 是一个如此简单的函数,所以我一定要 知道它的微商:我会不停地尝试直到求出它为止。”
1700948122
1700948123
但是你们发现找不到任何简单函数——用m 表示的、用m 的乘方以及这一类的函数,你们对这些函数进行微商时会给出1/m 。所以不知道用哪种方法时,我们要用另外的方法去做。这里我们要用数值积分来求它。
1700948124
1700948125
记住:每当你被数学分析难住时,你总能够用算术的方法来做 。
1700948126
1700948127
3-4 数值积分
1700948128
1700948129
让我们假定初始质量为10,并取简单近似,即每一次丢掉一个单位质量。进一步按以u 为单位测量所有的速度。因为这样我们就简单地得到Δv =Δm /m 。
1700948130
1700948131
我们想要求得累积的总速度。那好,让我们看看,在第一次抛弃一个单位的质量后获得了多少速率?这很容易,它是
1700948132
1700948133


1700948134
1700948135
1700948136
但这不完全对,因为在你们吐出一个单位质量的时候,反作用的质量不是10;当你们把一个单位质量全部喷出后,它只剩9。你们看,Δm 被射出去后,火箭的质量只有m -Δm ,所以最好把上式写成
1700948137
1700948138


1700948139
1700948140
1700948141


1700948142
但这还是不完全正确。如果火箭真的是一团一团地抛出物质,上式就是对的,但它不是——它是连续地抛出物质。在一开始,火箭的质量是10,在放出一个单位质量的末尾,它的质量仅为9——所以平均起来,它大致上是9.5。在第一个单位质量抛出的时间内,我们说质量m =9.5是反抗Δm =1的有效平均惯性质量,所以火箭得到一个等于 的反冲Δv :
1700948143
1700948144


1700948145
1700948146