1700956810
他意识到,倍周期分岔中的这些周期根本不是凭空出现的。它们被铺开在复平面上,不同的周期大小错落。总有一个周期 2、一个周期 4、一个周期 8 等处在视野之外,直到它们与实数直线相交。巴恩斯利匆忙从科西嘉岛赶回自己位于美国佐治亚理工学院的办公室,然后写作了一篇论文。他将这篇论文投给《数学物理学通讯》发表。该期刊的编辑碰巧是达维德·吕埃勒,而吕埃勒告诉了他一个坏消息。巴恩斯利无意中重新发现了一位法国数学家在五十多年前所做的一项工作。“吕埃勒把论文退了回来,就仿佛它是一块烫手山芋,并说道:‘迈克尔,你是在讨论朱利亚集合。’”巴恩斯利后来回忆道。2
1700956811
1700956812
2巴恩斯利。
1700956813
1700956814
吕埃勒还给了一个建议:“去找一下曼德尔布罗特吧。”
1700956815
1700956816
三年前,约翰·哈伯德,这位喜欢穿着花哨 T 恤的美国数学家正在位于巴黎西南奥尔赛的巴黎大学教授大一新生初等微积分。3 其中他会讲到的一个常规话题是牛顿法,一种通过渐次做出更好的近似来求解方程的经典方法。然而,哈伯德对于常规话题已经有点儿厌倦了,所以他决定这次尝试以一种会迫使学生进行思考的方式教授牛顿法。
1700956817
1700956818
3哈伯德;also Adrien Douady,“Julia Sets and the Mandelbrot Set,”in The Beauty of Fractals: Images of Complex Dynamical Systems, eds. H. - O. Peitgen and P. H. Richter (Berlin: Springer, 1986), pp. 161–174. 这本《分形之美》也给出了对于牛顿法以及我们这一章讨论到的复杂动力学的其他交叉领域的一个数学概述。
1700956819
1700956820
牛顿法由来已久,甚至在牛顿发明它之前就古已有之。古希腊人便使用过它的一个版本来寻找平方根。这种方法先从一个猜测开始。初始猜测引出一个更好的猜测,然后这个迭代过程不断重复,逐渐逼近一个答案,就像一个动力系统不断趋向其定态。这个过程收敛得很快,一般可以使得小数点后的精确位数每一步翻一倍。当然,现如今,求平方根可以用到更多数值分析方法,求二次方程(未知数的最高次数是二次的多项式方程)的所有根也是如此。但牛顿法也适用于更高次数的、无法直接求解的多项式方程。这种方法还被广泛用于各种计算机算法,毕竟迭代向来是计算机的强项。牛顿法的一个小小棘手之处在于,方程通常拥有不止一个解,尤其是需要考虑到复数解时,而这种方法会找到哪个解取决于初始猜测。在实践中,学生们发现这根本不成问题。你对于应该从何处开始一般有着很好的估计,而即便你的猜测看上去要收敛到一个错误的解,你也大可换个地方重新开始。
1700956821
1700956822
他们可能会好奇,牛顿法到底是以怎样一种方式逼近一个二次方程在复平面上的一个根的?从几何角度思考,一个可能的回答是,这种方法单纯只是找到两个根中更靠近初始猜测的那一个。这也是哈伯德一天在被问及这个问题时告诉他的学生的。
1700956823
1700956824
“至于比如三次方程,情况看上去要更为复杂,”哈伯德自信满满地说道,“我回去想一下,下周再告诉你们。”4
1700956825
1700956826
4“Julia Sets and the Mandelbrot Set,”p. 170.
1700956827
1700956828
他仍然设想,这时的困难之处会是教授他的学生如何计算迭代,而做出初始猜测则会是容易的。5 但他对此思考得越多,他发现自己了解得越少——对于什么才算一个聪明的猜测,或者更进一步地,对于牛顿法究竟是怎样运作的。那个显而易见的几何化猜想会将复平面平分成三个扇形,每个扇形包含一个根,但哈伯德发现情况并没有这样简单。奇怪的事情发生在靠近边界的地方。此外,哈伯德还发现自己并不是第一位邂逅这个出人意料困难的问题的数学家。阿瑟·凯莱曾在 1879 年尝试将容易处理的二次方程情况扩展到极难解决的三次方程情况。不过,在一个世纪后,哈伯德手头拥有了凯莱当时所没有的一件工具。
1700956829
1700956830
5哈伯德。
1700956831
1700956832
哈伯德属于这样一类数学家,他们鄙弃猜测、近似、基于直觉而非证明的半吊子真理。他也属于这样一批数学家,他们会在爱德华·洛伦茨的吸引子见诸科学文献的二十多年后仍然坚持认为,没有人知道这些方程是否真的会生成这样一个吸引子。它还是一个未经证明的猜想。他会说,大家熟悉的双螺旋并不是证明,而不过是证据,只是计算机画出来的某种东西。
1700956833
1700956834


1700956835
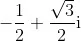
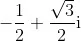
1700956836


1700956837
尽管如此,他现在还是开始试着利用计算机做些原来的正统数学方法所没有做过的事情。计算机证明不了任何东西,但至少它可能揭示出真理,使得数学家可以知道自己应该试图证明什么。所以哈伯德开始进行数值实验。他不是将牛顿法视为一种解决问题的方法,而是将它本身视为一个问题。哈伯德考虑的是一个三次方程的最简单的例子——方程 ,也就是说,求 1 的立方根。当然,在实数域,它只有一个平凡解:1。但这个多项式方程还有两个复数解: 和 。画在复平面上,这三个根构成了一个等边三角形,其中一个点位于三点钟方向,一个点位于七点钟方向,另一个点位于十一点钟方向。现在的问题是,给定任意一个复数作为起始点,看看牛顿法最终会得出这三个解中的哪一个。这就好像牛顿法是一个动力系统,而三个解是三个吸引子;又或者说,这就好像复平面是平滑过渡到三个深谷的一个表面。一颗玻璃球,不论被放在表面上的哪一点,都应该滚进这三个谷地中的一个——但具体是哪一个呢?
1700956838
1700956839
哈伯德开始从构成复平面的无穷多个点中采样。他让计算机一一处理这些点,计算出在每种情况下使用牛顿法的结果,并用不同颜色对不同结果编码。最终会得出第一个解的所有起始点用蓝色标出,最终趋向第二个解的点标为红色,生成第三个解的点则标为绿色。他发现,在最粗略的近似下,牛顿法的动力学确实将整个复平面平分成了三个扇形。在一般情况下,那些更靠近某个解的点很快会得出那个解。但系统的计算机探索这时也揭示出了一些更为复杂的行为,而它们是先前那些只能这里计算一个点、那里计算一个点的数学家从未见过的。尽管有些初始猜测很快收敛到一个根,但有些点在最终收敛到一个解之前要先看似随机地跳来跳去一番。有时候,似乎一个点可以落入一个永远不断重复自己的循环(一个周期性循环)当中,而不会趋向三个解中的任何一个。
1700956840
1700956841
随着哈伯德驱使他的计算机去探索越来越精细的细节,从中开始浮现出来的图案让他和他的学生深感困惑。比如,在蓝色与红色谷地之间,他看到的不是一条泾渭分明的分水岭,而是一些绿色的斑块,犹如一串宝石点缀其间。这就好像一颗玻璃球,在相邻两个谷地争夺不下的时候,却最终落入了最遥远的第三个谷地。在两种颜色之间终究无法充分形成一条边界。6 在进一步放大检视下,一个绿色斑块与蓝色谷地之间的曲线被证明也具有红色的斑块,如此等等。这里的边界最终向哈伯德揭示出了一个奇特性质,让即便看惯了曼德尔布罗特的怪异的分形图案的人也不免感到疑惑:没有一个点是仅两种颜色之间的一个边界。只要两种颜色试图走到一起,第三种颜色就会介入,将一系列新的、自相似的成分插入其间。不可思议的是,每个边界点都邻接所有三种颜色的各一个区域。
1700956842
1700956843
6哈伯德;The Beauty of Fractals; Peter H. Richter and Heinz - Otto Peitgen,“Morphology of Complex Boundaries,”Berichte der Bunsengesellschaft für Physikalische Chemie 89 (1985), pp. 575–588.
1700956844
1700956845


1700956846
1700956847
1700956848
© Heinz-Otto Peitgen, Peter H. Richter
1700956849
1700956850
具有无穷复杂性的边界
1700956851
1700956852
当一个派被切成三块扇形小块时,它们只在一个点三块相交,而任意两块之间的边界也简单明了。但抽象数学以及现实世界物理学中的许多过程最终被证明可以生成几乎不可想象的复杂性。
1700956853
1700956854
在上面的图中,被用于求 -1 的立方根的牛顿法将复平面分成了三个相等的区域,其中一个用白色标出。所有的白色点都被“吸引”到位于最大的白色区域内的根,所有的黑色点都被吸引到另外两个根之一。这里的边界具有一个奇特性质,即每个边界点都邻接所有三个区域。并且正如局部放大图所显示的,放大后的部分具有一种分形结构,在越来越小的尺度上不断重复原来的基本模式。
1700956855
1700956856
哈伯德就这些复杂形状及其数学意涵展开了研究。他及其同事的工作很快开辟出了动力系统研究的一条新战线。他意识到,牛顿法的作图只是一大类尚未得到探索的、反映了现实世界中的行为模式的图案之一。迈克尔·巴恩斯利也正在研究这个家族的其他成员。而正如这两人很快会了解到的,贝努瓦·曼德尔布罗特则正在研究所有这些形状的“老祖宗”。
1700956857
1700956858
曼德尔布罗特集合 7 是数学中最复杂的对象,其推崇者常常喜欢这样说。8 即便永恒的时间也不足以将它穷尽,看遍其圆盘上参差的凸起(“原子”)、凸起上卷起的螺旋、螺旋上挂着的球状分子——它们就像上帝的私人葡萄藤上结的葡萄,排布变化万千。在计算机屏幕上不断放大其局部,曼德尔布罗特集合看上去要比分形更分形,在每个尺度上都有着如此丰富的复杂性。要想为其中的不同图案进行编目,或者对集合的轮廓给出一个数值描述,无疑需要用到无穷多的信息。但一个悖论出现了:要想传递该集合的一个完整描述,却只需要传输一段数十个字符的代码。一段简短的计算机程序就包含足够的信息来重现整个集合。这种集复杂性和简单性于一身的做法让最早一批意识到这一点的研究者都不禁深感意外——甚至曼德尔布罗特也不例外。曼德尔布罗特集合后来成为混沌的某种公共符号,出现在会议手册和工程季刊的封面上,充当着一个在 1985 年和 1986 年到世界各地展出的计算机艺术展的重头戏。其美丽很容易就从这些图案上感受到,其含义则要更难把握到,数学家也是慢慢才开始理解。
1700956859