1700974750
图 1-27
1700974751
1700974752
刚体作任意运动时,可随意选取一个点部位C,将刚体的运动分解成随C的平动和绕C的转动.月球相对地球的运动,可分解成月球随球心C围绕地球的圆轨道平动和月球绕着过C点几何轴的转动.C绕地球的圆轨道周期与月球绕C转动周期相同,使得月球如图1-28所示,某半个球面(图中空白区域)始终对着地球,另外半个球面(图中斜线区域)始终背着地球.
1700974753
1700974754


1700974755
1700974756
1700974757
图 1-28
1700974758
1700974759
刚体运动分解时,平动参考点的选取虽可任意,实际上总会根据具体问题视方便选取.形状对称的刚体,从运动学方面考虑,常选中央点为平动参考点.(从动力学方面考虑,更愿选取质心为平动参考点.)例如自行车轮在地面上的纯滚动,通常分解成随车轮中心的平动和绕过中心水平轴的转动.许多刚体,中心处没有该刚体的物质分布,自行车轮便是一例.如果将刚体引申为可以无限延展的刚性物体,延展部位密度等于零,或者说任何一个与刚体各点部位始终保持相对静止的点均可属刚体“所有”,那么刚体几何中心处即使没有该刚体的物质分布,仍可属刚体的点.这样引申后,进而可据需要指称原刚体外任何一个相对它静止的点为属于该刚体的点.
1700974760
1700974761
1700974762
1700974763
1700974764
力学(物理类) [:1700973446]
1700974765
力学(物理类) 1.5 参考系间的相对运动
1700974766
1700974767
1.5.1 参考系间的平动
1700974768
1700974769
物体间有相对运动,参考系间也有相对运动,参考系间的相对运动与刚体运动一样,可分解为相互间的平动和转动.
1700974770
1700974771
参考系对其他物体运动的描述,都可归结为对质点运动的描述.参考系S′和S间若存在相对运动,则需要研究同一质点在S′和S系的运动学量之间有什么样的关联.
1700974772
1700974773
首先讨论S′和S间有相对平动.在S′系和S系中分别构置直角坐标系O′x′y′z′和Oxyz,为方便,设x′与x,y′与y,z′与z分别平行,如图1-29所示.S′系相对S系的平动,可用O′点在S系中的运动
1700974774
1700974775
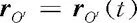
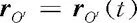
1700974776
1700974777
1700974778


1700974779
1700974780
1700974781
图 1-29
1700974782
1700974783
表述.应当强调,O′在S系中的运动可以是直线的,也可以是曲线的.将某质点P在S′,S系中的运动方程分别记作
1700974784
1700974785


1700974786
1700974787
1700974788
经典力学中设定
1700974789
1700974790


1700974791
1700974792
1700974793
结合图1-29,可得运动方程间的关联式:
1700974794
1700974795


1700974796
1700974797
1700974798
分量式为
1700974799