1700975907
在S系中无论是哪两个质点,无论各自处于何种运动状态,无论其间距离r为多大,G是相同的常量.同样,在S′系无论是哪两个质点,无论各自处于何种运动状态,无论其间距离r′为多大,G′是相同的常量.取两个特定的质点,处于一组特殊的状态,来确定G与G′的关系.万有引力公式中的质量已等效处理成惯性质量,这两个质点在S,S′系的质量相同,即已有.先将这两个质点静放在S系中相距r,测得其间引力大小为F,再将它们静放在S′系中相距r′=r,测得其间引力大小为F′.系统在S系的状态与在S′系的状态相同,据相对性原理,必有F=F′,于是得
1700975908
1700975909


1700975910
1700975911
1700975912
即引力常量G是惯性系不变量.
1700975913
1700975914


1700975915


1700975916
电相互作用内容丰富,不作全面讨论,只考虑其中的库仑定律.前已指出,库仑定律只适用于“施力电荷”Q是静电荷的情况,这与牛顿万有引力定律是不同的.库仑定律中,真空介电常量ε0是力常量,作为实验的总结,定律必能在某个参考系中成立,在此参考系中无论对哪一个“施力电荷”Q和哪一个静止的或运动的“受力电荷”q,ε0是相同的常量.假设库仑定律符合经典力学相对性原理要求,那么在惯性系S中ε0是相同常量,在惯性S′中也是相同常量.为获得ε0与间的关系,任取一对“施力电荷”和“受力电荷”,在S系中令两者均处于静止状态,电量分别为Q,q,若在S′系中两者都处于静止状态,各自电量必为Q′=Q,q′=q,这也意味着S,S′系电量单位一致.在S系中两者相距r,库仑力大小为
1700975917
1700975918


1700975919
1700975920
1700975921
在S′系中使两者也相距r′=r,库仑力大小为
1700975922
1700975923


1700975924
1700975925
1700975926
据相对性原理要求,必有F=F′,即得
1700975927
1700975928


1700975929
1700975930
1700975931
这表明,如果库仑定律符合经典力学相对性原理要求,那么真空介电常量ε0,作为力常量,必定是惯性系不变量.
1700975932
1700975933
1700975934
1700975935
1700975936
力学(物理类) [:1700973452]
1700975937
力学(物理类) 2.4 惯性力
1700975938
1700975939
牛顿第二定律和它的时空定量展开,即冲量—动量关系、功—能关系、力矩—角动关系,将构成牛顿力学的主体内容.惯性系中各类力学问题的定量处理,多是依据第二定律和这三个基本关系进行的.非惯性系中第二定律不成立,质点质量m与质点在非惯性系加速度a′的乘积,不等于质点所受真实力F.如果引入虚拟的或者说假想的力F虚,使得
1700975940
1700975941
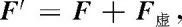
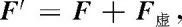
1700975942
1700975943
1700975944
能满足关系式
1700975945
1700975946
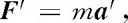
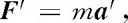
1700975947
1700975948
1700975949
上式的数学内容与第二定律同构.因此便可将第二定律及其时空展开关系移用到非惯性系,直接处理非惯性系中出现的若干力学问题,不必事事都还原到惯性系去处理.需要注意的只是F虚并非真实力,不存在第三定律提及的反作用力.虚拟力F虚又常称为惯性力,F虚与真实力F之和F′称为表观力.
1700975950
1700975951
经常会接触到变速平动非惯性系,在直轨道上变速行驶的列车便是一例,后文将涉及的质心系又是一例.考虑到地球的自转,地面参考系其实是匀速旋转非惯性系.这两类参考系中要引入的惯性力分别是平移惯性力和惯性离心力、科里奥利力.
1700975952
1700975953
2.4.1 平移惯性力
1700975954
1700975955
设非惯性系S′相对于惯性系S作变速平动,如图2-16所示,图中加速度a0未必是常矢量.质点m相对于S系的加速度设为a,S系据牛顿第二定律判定质点受真实力
1700975956