1700976286
使得
1700976287
1700976288
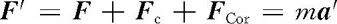
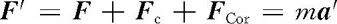
1700976289
1700976290
1700976291
成立.FCor由法国学者科里奥利(G. Coriolis)于1835年首先提出,故命名为科里奥利力.
1700976292
1700976293
科里奥利力因质点相对于S′系运动而引入,上面的表达式却未能表现质点运动因素,试着改造.按通常习惯,在右手系中将角速度ω矢量化为ω,方向垂直于图2-26平面向上.质点相对于S′系的速度v′方向也已在图中示出,大小为ωr′,可得
1700976294
1700976295


1700976296
1700976297
1700976298
科里奥利力便可改述成
1700976299
1700976300


1700976301
1700976302
1700976303


1700976304


1700976305


1700976306
(2.27)式是科里奥利力的普遍表述式,无论质点m相对S′系取什么样的速度v′,对应的科里奥利力均由(2.27)式给出.将v′按图2-27实线所示,分解为角向分量,径向分量和轴向分量,则有
1700976307
1700976308


1700976309
1700976310
1700976311


1700976312
1700976313
1700976314
图 2-27
1700976315
1700976316


1700976317
图2-26所示为仅有角向速度对应的科里奥利力FCor(θ).
1700976318
1700976319


1700976320


1700976321
任何情况下轴向速度对应的科里奥利力均为零,即FCor(z)=0.这是很好理解的,因为质点沿轴向的分运动在S′系和在S系是一致的,故S′系中轴向虚拟力必为零.径向速度对应的科里奥利力FCor(r),需要作简单解释.
1700976322
1700976323
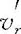
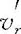
1700976324


1700976325


1700976326
参照图2-28,径向朝外时对应的FCor(r)方向与S′系相对于S系旋转方向相反.设质点m在S′系没有角向运动,沿FCor(r)方向的加速度aθ=0,必有与FCor(r)大小相同,方向相反的真实力Fθ存在,这一真实力需在惯性系S中寻找.参阅图2-29,设t时刻质点在S′系中位于r′处,相对于S系具有角向速度,大小为ωr′.经dt时间,S′系原径向线相对于S系转过角度dθ=ωdt,质点到达r′+dr′位置,其中.此时新的角向速度方向如图2-29示,大小为ω(r′+dr′),新的径向速度方向也已在图中示出,大小为.图2-29中竖直虚线代表t时刻的角向方位线,t到t+dt时间内,质点相对于S系在此方向线上的速度增量为
1700976327
1700976328


1700976329
1700976330
1700976331


1700976332
1700976333
1700976334
图 2-28
1700976335