1700978100
1700978101
1700978102
式中λ为绳的质量线密度.可解得
1700978103
1700978104


1700978105
1700978106
1700978107
绳的水平方向动量便为
1700978108
1700978109


1700978110
1700978111
1700978112
px从零增加到极大值时,N对应降到零.从上式很易确定l=L/2时,px达极大,绳将甩离桌面棱边.
1700978113
1700978114
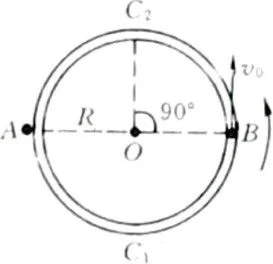
例10 如图3-24所示,半径R的水平凹形圆槽绕着圆周上的A点匀速旋转,在直径AOB的B处放一小球,小球与槽的侧壁光滑接触,与图中AC1B半圆槽底部也光滑接触,与BC2A半圆槽底部有摩擦,摩擦因数处处相同.开始时小球相对圆槽有切向初速v0.小球经过BC2A半圆以近似为零的相对速度通过A点,继而又绕过四分之三圆周到达C2点时速度恰好降为零.
1700978115
1700978116

1700978117
1700978118
1700978119
图 3-24
1700978120
1700978121
(1)试求圆槽绕A点旋转角速度ω和小球与BC2A半圆槽底部间的摩擦因数μ;
1700978122
1700978123
(2)判定小球到达C2点后能否停留在该处,若不能,小球将朝哪一个方向运动?
1700978124
1700978125
解 (1)圆槽参考系是匀速旋转非惯性系,惯性离心力对应离心势能,科里奥利力不作功.将小球初位置B与到达的位置A和后来又到达的位置C分别联系起来,可建立两个功能关系式:
1700978126
1700978127


1700978128
1700978129
1700978130
式中m为小球质量.由此可解得
1700978131
1700978132


1700978133
1700978134
1700978135
(2)小球在C2处的惯性离心力水平向右切向分量为
1700978136
1700978137


1700978138
1700978139
1700978140
C2处的最大静摩擦力和滑动摩擦力为
1700978141
1700978142


1700978143
1700978144
1700978145
因此小球到达C2点后不能停留在该处,而会朝右后退运动.
1700978146
1700978147
1700978148
1700978149