1700978200
足球碰墙弹回,便属此例.
1700978201
1700978202
●完全非弹性碰撞
1700978203
1700978204
碰后质点1和2一起运动,可补充方程并得解
1700978205
1700978206


1700978207
1700978208
1700978209
可算得碰后动能损失
1700978210
1700978211


1700978212
1700978213
1700978214
●非弹性碰撞
1700978215
1700978216
介于弹性与完全非弹性之间的碰撞称为非弹性碰撞,此类碰撞可引入恢复系数
1700978217
1700978218


1700978219
1700978220
1700978221
来描述.(3.46)式联立(3.41)式,解得
1700978222
1700978223


1700978224
1700978225
1700978226
碰后动能损失量
1700978227
1700978228


1700978229
1700978230
1700978231
小于完全非弹性碰撞的动能损失量.
1700978232
1700978233
恢复系数e与物体结构有关,弹性碰撞的物体可以认为e=1,完全非弹性碰撞的物体可以认为e=0.
1700978234
1700978235
质点化三体一维碰撞前后运动状态如图3-26(a)(b)所示,动量守恒式为
1700978236
1700978237


1700978238
1700978239
1700978240


1700978241
1700978242
1700978243
图 3-26
1700978244
1700978245
若碰撞是完全非弹性的,补充方程
1700978246
1700978247
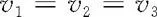
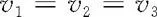
1700978248
1700978249