1700981251
结构对称的常见刚体,相对于过中心转轴的转动惯量,列于表5-1.其中匀质长方体的参量l1=l2=h时,便成匀质立方体;l2趋于零时,便成匀质长方板;l2,h均趋于零时,便成匀质细杆.薄圆筒质量可以是均匀分布,也可以不是均匀分布;圆筒高度趋于零时,便成细圆环.匀质圆筒的R2趋于零时,便成匀质圆柱体;高度趋于零时,便成有宽度的匀质圆环或者匀质薄圆板.匀质球壳的R2趋于零时,便成匀质球体;R2趋于R1时,便成匀质薄球壳.
1700981252
1700981253
表5-1 常见刚体的转动惯量
1700981254
1700981255


1700981256
1700981257
1700981258


1700981259
刚体相对于某转轴的转动惯量I,总可表述成刚体质量m与某个长度量平方的乘积,将这一长度量记为,则有
1700981260
1700981261


1700981262
1700981263
1700981264


1700981265


1700981266


1700981267


1700981268
称为刚体相对于此转轴的回转半径.设想刚体质量m全部集中在与转轴相距的点部位,构成的假想质点相对于该转轴的转动惯量便是.各边长l的匀质长方体,相对于过中心转轴的回转半径.半径R的匀质球体,相对于过球心转轴的回转半径.
1700981269
1700981270


1700981271
例9 质点系动能Ek可分解为质心动能EkC与质点系相对质心动能之和,试据此导出刚体平行轴定理.
1700981272
1700981273
解 参考图5-17,设质量m的刚体绕固定轴MN的转动角速度为ω,转动动能便是
1700981274
1700981275


1700981276
1700981277
1700981278
质心速度和质心动能分别是
1700981279
1700981280


1700981281
1700981282
1700981283


1700981284
刚体相对于质心动能即为刚体在质心系中绕PQ轴的转动动能.刚体绕PQ轴转动角速度也是ω,故有
1700981285
1700981286


1700981287
1700981288
1700981289
由
1700981290
1700981291


1700981292
1700981293
1700981294
即得
1700981295
1700981296
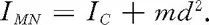
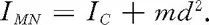
1700981297
1700981298
1700981299
例10 质量m,两边长分别为a和b的匀质长方板,相对于过中心O且与板面垂直轴的转动惯量I0,从量纲上考虑必可表达成
1700981300