1700986342


1700986343
1700986344
1700986345
解得
1700986346
1700986347
b21, b22=-2b21, b23=b21.
1700986348
1700986349
(7.50)式中系数b31,b32,b33的求解:
1700986350
1700986351
将ω2(3)=0代入类(7.52)式(即以b31,b32,b33分别替换b11,b12,b13),可得
1700986352
1700986353


1700986354
1700986355
1700986356
解得
1700986357
1700986358


1700986359
1700986360
1700986361
(7.50)式中系数x1,x2,x3的求解:
1700986362
1700986363
将上述解得的系数b11,b12,…,b32,b33代入(7.50)式,可得
1700986364
1700986365
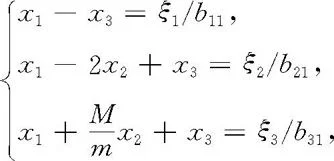
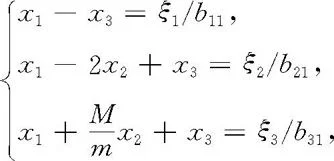
1700986366
1700986367
1700986368
解得
1700986369
1700986370


1700986371
1700986372
1700986373
由(7.51)式给出的ξ1,ξ2,ξ3通解为
1700986374
1700986375


1700986376
1700986377
1700986378
也可引入新的待定常量A1,A2,a,b,将这些通解改述成
1700986379
1700986380
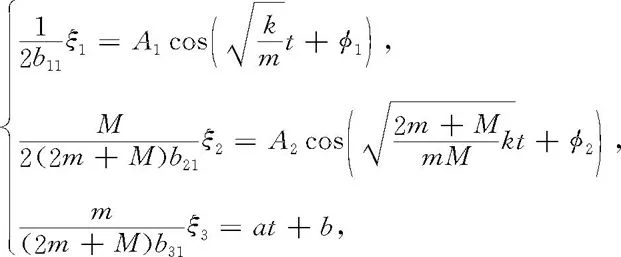
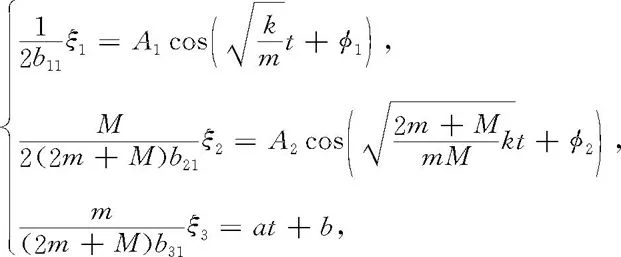
1700986381
1700986382
1700986383
于是x1,x2,x3的通解各为
1700986384
1700986385


1700986386
1700986387
1700986388


1700986389


1700986390
据此可见,简正模在x1,x3中对应的振动量大小相同,方向相反,x2则不参与该模的振动,系统质心不动,如图7-42(a)所示.简正模在x1,x3中对应的振动量大小和方向都相同,x2中对应的振动量方向相反,振动量大小可确保系统质心不动,如图7-42(b)所示.ω(3)=0简正模在x1,x2,x3中对应的运动量实为随系统质心一起作平动,如图7-42(c)所示.
1700986391