1700986377
1700986378
也可引入新的待定常量A1,A2,a,b,将这些通解改述成
1700986379
1700986380
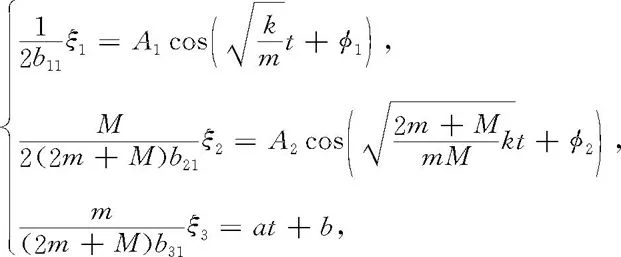
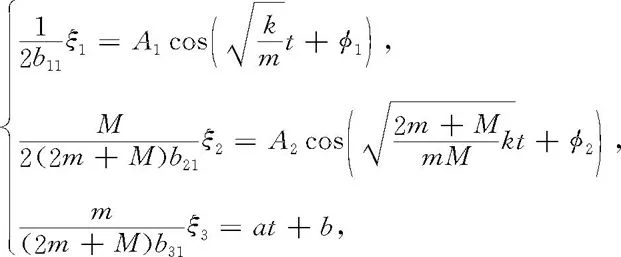
1700986381
1700986382
1700986383
于是x1,x2,x3的通解各为
1700986384
1700986385


1700986386
1700986387
1700986388


1700986389


1700986390
据此可见,简正模在x1,x3中对应的振动量大小相同,方向相反,x2则不参与该模的振动,系统质心不动,如图7-42(a)所示.简正模在x1,x3中对应的振动量大小和方向都相同,x2中对应的振动量方向相反,振动量大小可确保系统质心不动,如图7-42(b)所示.ω(3)=0简正模在x1,x2,x3中对应的运动量实为随系统质心一起作平动,如图7-42(c)所示.
1700986391
1700986392


1700986393
1700986394
1700986395
图 7-42
1700986396
1700986397


1700986398


1700986399
x1,x2,x3通解中的6个待定常量A1,1,A2,2,a,b,可由t=0时刻图7-41中小物块1,2,3的位置和速度确定.
1700986400
1700986401
1700986402
1700986403
1700986404
力学(物理类) [:1700973483]
1700986405
力学(物理类) 7.4 阻尼振动 受迫振动 自激振动
1700986406
1700986407
7.4.1 阻尼振动
1700986408
1700986409
物体在回复性保守力作用下可在其平衡位置周围振动,真实情况下物体还会受到各种阻力,使得振动逐渐减弱,最终停下.阻力较大时,物体甚至振动不起来,只能从初始位置单调缓慢地移向平衡位置.力学中将物体在回复性保守力和阻力共同作用下的运动,称为阻尼振动.
1700986410
1700986411
将讨论范围限于直线方向的阻尼振动,回复性保守力Fx取为线性力,阻力fx取为流体中的黏力,即有
1700986412
1700986413


1700986414
1700986415
1700986416
设振子质量为m,则动力学方程为
1700986417
1700986418


1700986419
1700986420
1700986421
为适应数学处理的规范性,也可改述成
1700986422
1700986423


1700986424
1700986425
1700986426
称γ为阻力系数,β为阻尼系数,ω0为固有角频率(也有简称为固有频率的).