1700986593
得
1700986594
1700986595


1700986596
1700986597
1700986598
表明在阻尼很小的情况下,描述阻尼能耗的品质因素Q与固有频率ω0成正比,与阻尼系数β成反比.
1700986599
1700986600
从图7-43,7-44,7-45可以看出,仅在低阻尼情况下,振子的运动仍然具有振动的基本特征,只是振幅不断衰减,振动越来越弱,最终停止在力平衡点.因此,若无特殊说明,通常所谓的阻尼振动均指低阻尼振动.
1700986601
1700986602
例18 试由t=0时振子的位置x0和速度v0,确定过阻尼振动(7.57)式中的常量A1和A2.
1700986603
1700986604
解 据(7.57)式,有
1700986605
1700986606
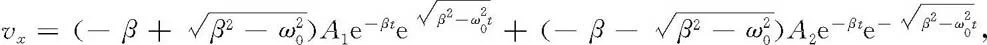
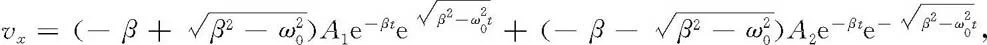
1700986607
1700986608
1700986609
结合初条件,可得
1700986610
1700986611


1700986612
1700986613
1700986614
解得
1700986615
1700986616


1700986617
1700986618
1700986619


1700986620
1700986621
1700986622
例19 一个弹簧振子的质量m=5.0kg,低阻尼情况下振动频率为f=0.50Hz,已知振幅的对数减缩λ=0.02,试求弹簧的劲度系数k.再问,阻尼系数β取何值时,能使振子在最短的时间内基本上停止运动?
1700986623
1700986624
解 据λ=βT=β/f,可得此时β=λf=0.01s-1,所求弹簧的劲度系数为
1700986625
1700986626


1700986627
1700986628
1700986629
临界阻尼时振子可在最短时间内基本上停止运动,因β≪f,故ω0≈ω,此时应有
1700986630
1700986631


1700986632
1700986633
1700986634
7.4.2 受迫振动
1700986635
1700986636
阻尼振动中随着能量的损耗,物体最终将停止运动.如果在保守性回复力和阻尼力之外,另有一个力通过对物体作功不断输入能量,那么物体仍可保持连续的振动.外加的力若是周期性的,例如由于钟表内的擒纵机构提供推动力,车辆在平直道路上近匀速行驶中车身受到小幅度颠簸力,形成的振动称为受迫振动.
1700986637
1700986638
受迫振动中周期性的外力称为驱动力,借助傅里叶级数理论,任一驱动力均可展开成一系列简谐力的叠加,因此最基本的驱动力可表述为
1700986639
1700986640


1700986641
1700986642