1700986627
1700986628
1700986629
临界阻尼时振子可在最短时间内基本上停止运动,因β≪f,故ω0≈ω,此时应有
1700986630
1700986631


1700986632
1700986633
1700986634
7.4.2 受迫振动
1700986635
1700986636
阻尼振动中随着能量的损耗,物体最终将停止运动.如果在保守性回复力和阻尼力之外,另有一个力通过对物体作功不断输入能量,那么物体仍可保持连续的振动.外加的力若是周期性的,例如由于钟表内的擒纵机构提供推动力,车辆在平直道路上近匀速行驶中车身受到小幅度颠簸力,形成的振动称为受迫振动.
1700986637
1700986638
受迫振动中周期性的外力称为驱动力,借助傅里叶级数理论,任一驱动力均可展开成一系列简谐力的叠加,因此最基本的驱动力可表述为
1700986639
1700986640


1700986641
1700986642
1700986643


1700986644
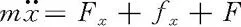
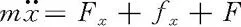
1700986645
振子质量记为m,所受回复性保守力和阻尼力仍取为线性力,即,受迫振动的动力学方程可改述成
1700986646
1700986647
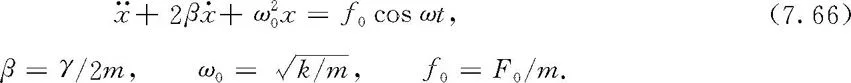
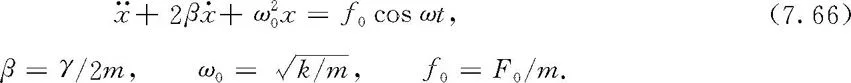
1700986648
1700986649
1700986650
(7.66)式是一个非齐次的常系数线性微分方程,它的通解x(t)也包含两个可由初条件确定的常量.如果找到一个特殊的非齐次解x*(t),再将非齐次方程对应的齐次式
1700986651
1700986652


1700986653
1700986654
1700986655
的通解记为x0(t),那么很容易看出,
1700986656
1700986657


1700986658
1700986659
1700986660
也必定是非齐次方程的一个解.考虑到x0(t)中已包含两个待定常量,因此合成的x(t)即为非齐次方程的通解.x0(t)实为阻尼振动通解,已在前面给出.非齐次特解可猜测为
1700986661
1700986662


1700986663
1700986664
1700986665
代入(7.66)式,可得
1700986666
1700986667


1700986668
1700986669
1700986670
因特解应在任意t时刻都成立,故上式两边cosωt和sinωt的系数应分别相等,即有
1700986671
1700986672


1700986673
1700986674
1700986675
解得
1700986676