1700988818
至此,各惯性系取同一把理想直尺建立了自身的空间度量系统,又依据光速不变原理建立了各自的时间度量系统.
1700988819
1700988820
二、惯性系间时空度量的相对性
1700988821
1700988822
每一个惯性系可依据光速不变原理建立自身的时间度量系统,但各自认定的是光相对本惯性系的真空传播速度为常量c,而光相对其他惯性系的真空传播速度却并不是c.于是,便会引发惯性系之间时空度量的差异,这就是时空度量相对性的表现.
1700988823
1700988824
(1)时钟零点校准的差异(“同时”的相对性)
1700988825
1700988826
设惯性系S,S′间的相对运动关系如图8-5所示,令坐标原点O,O′相遇时刻,S系中将静止在O点的时钟拨到t=0,S′系中将静止在O′点的时钟拨到t′=0,使两个惯性系之间有了共同的计时零点.
1700988827
1700988828


1700988829
1700988830
1700988831
图 8-5
1700988832
1700988833


1700988834


1700988835
S,S′系各自为校准其他时钟零点,可在O,O′相遇处放置光源P,在O,O′相遇时刻,P沿着图8-5中的左、右两个方向分别发出光信号.S系中如果x轴上的A,B两点与O点的间距都是1个长度单位,那么A,B各自在接收到光信号时,可分别将静止在A,B的时钟拨到1个单位的读数上.为了方便,将1个单位时间说成1小时,则A,B时钟读数均为1:00.S′系中如果x′轴上的A′,B′两点与O′也相距1个长度单位,那么A′,B′各自在接收到光信号时也分别将自己的静止时钟拨到1:00.需要强调,S系不仅认为自己应当用这样的方法校准各处时钟零点,而且还认定S′系也应当用这样的方法校准S′系中各处时钟零点.然而其间存在差异,因为S系认为光相对S′系中A′的速度是c-v,传送到A′所需时间应大于1个单位时间,譬如说是1小时10分.故按S系计时系统,A′接收光信号的时刻为tA′=1:10,但S′系已将A′时钟拨到.相互比较,于是S系认为S′系中A′时钟读数拨快了.S系还认为光相对B′的速度为c+v,按S系计时系统,B′接收光信号的时刻,譬如说应为tB′=0:51′26″,与比较,S系认为S′系中B′时刻读数拨慢了.同样的分析,可知S′系认为S系中A时钟的读数(1:00)拨快了(应为0:51′26″),B时钟的读数(1:00)拨慢了(应为1:10).这就是惯性系之间时钟零点校准的差异.
1700988836
1700988837
时钟零点校准的差异与同时的相对性是一致的.S′系中认为O′时钟读数显示为1:00的事件和光信号到达A′事件以及光信号到达B′事件是同时发生的,因此A′,B′时钟应与O′时钟一致地指示在1:00.S系则认为这三个事件不是同时发生的,其中第三个事件发生得最早(0:51′26″),第二个事件发生得最晚(1:10).顺便一提,O′时钟读数为1:00的时刻,在S系的计时系统中并非对应1:00,而是tO′>1:00(由后文给出的定量变换公式可知tO′=1:0′43″),这是因为S系认为O′时钟的计时率会因运动而变慢.
1700988838
1700988839
(2)运动直尺的长度收缩(空间间距度量的相对性)
1700988840
1700988841


1700988842
直尺A′B′静止在S′系的x轴上,两个端点的坐标之间的差值即为直尺的静止长度,即有
1700988843
1700988844


1700988845
1700988846
1700988847
直尺相对S系是运动的,S系中测量运动直尺长度的一个可取方案是在同一时刻测定动点A′,B′在x轴上的坐标,这两个坐标量之间的差值即为直尺的运动长度.例如在S系计时系统中如图8-6所示,测得A′在t1=1:00时刻位于x1,B′在t2=1:00时刻位于x2,便有
1700988848
1700988849


1700988850
1700988851
1700988852


1700988853
1700988854
1700988855
图 8-6
1700988856
1700988857
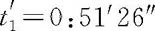
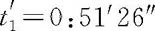
1700988858


1700988859
据前所述,S′系按自己的计时系统认定x1,x2两处时钟零点校准有差异,x1处时钟拨快了(t1=1:00对应S′系计时系统),x2处时钟拨慢了(t2=1:00对应S′系计时系统).S′系认为因相对运动这种先测头部A′位置,后测尾部B′位置的必然结果是
1700988860
1700988861


1700988862
1700988863
1700988864
这就是运动直尺的长度收缩.l静即为S′系中两个静止点之间的空间间距度量值,l动则是S系中这两个运动点之间的空间间距度量值,l动≠l静正是惯性系之间空间间距度量相对性的表现.
1700988865
1700988866
(3)运动时钟计时率的变慢(时间间隔度量的相对性)
1700988867