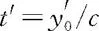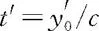1700988993
设t=t′=0时在O,O′重合处,沿x,x′轴发出一个光信号,光信号于某时刻到达某一空间位置的点事件,在S,S′系的时空坐标分别为{x=ct,t},{x′=ct′,t′}.代入(8.2)式,得
1700988994
1700988995


1700988996
1700988997
1700988998
再将②式代入,得
1700988999
1700989000


1700989001
1700989002
1700989003
联立①②③④b式,可解得
1700989004
1700989005


1700989006
1700989007
1700989008
将(8.5)式代入(8.2)式,并结合(8.1)式,便得狭义相对论的时空变换:
1700989009
1700989010


1700989011
1700989012
1700989013
由于历史原因,这一变换也称为洛伦兹变换.将(8.5)式代入(8.3)式,并结合(8.1)式,可得(8.6)式的逆变换:
1700989014
1700989015


1700989016
1700989017
1700989018


1700989019


1700989020


1700989021


1700989022


1700989023


1700989024
(8.6)和(8.7)中的时间变换式给出了时钟零点校准差异的定量关系式.S′系中x′轴上各时钟同时指零,即有t′=0,但按照S系的计时系统,除去x′=0点对应t=0外,其余均对应t≠0.将c记成1个速度单位,设个速度单位,S′系中(1个长度单位)、(-1个长度单位)三处,时钟读数如果同为1个时间单位(例如1:00),那么对应S系中的时间便分别为个时间单位(例如1:0′43″),个时间单位(例如1:10),个时间单位(例如0:50′26″).这就是前文图8-5所示范例的定量解释.
1700989025
1700989026
从洛伦兹变换式可以看出,惯性系之间的相对运动须受v<c的限制.参考系与参考物联系在一起,因此在任一惯性系中物体的运动速度都受v<c的限制.光束是物质,它的真空速度为c,但光束不是物体,不可取为参考物,不可构成度量其他物体运动的参考系.
1700989027
1700989028


1700989029


1700989030
参考系间的相对速度v≪c时,如果(8.6)式可近似为
1700989031
1700989032


1700989033
1700989034
1700989035
即过渡到伽利略变换.可见,经典的时空度量变换是狭义相对论时空度量变换的低速近似.
1700989036
1700989037
例1 洛伦兹变换中的时间变换式与y,y′,z,z′无关,表明时钟零点校准差异只发生在S,S′系的x,x′轴上,而不会发生在y,y′(或z,z′)轴上.试用光速不变原理予以验证.
1700989038
1700989039


1700989040


1700989041


1700989042