1700995016
= 9的倍数 + (27 + 3)
1700995017
1700995018
=9的倍数+ 3
1700995019
1700995020
尽管除法没有用弃九法检验答案正确与否的惯例,但是我忍不住想向大家介绍一种神奇的方法,来解决除数是9的除法问题。有人把这种方法称作“吠陀法”(Vedic)。我们来看下面这道题:
1700995021
1700995022
12 302 ÷ 9
1700995023
1700995024
先把它写成这种形式:
1700995025
1700995026
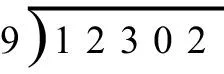
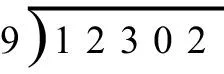
1700995027
1700995028
1700995029
接下来,把首位数放到横线之上,在最后一位数上方写一个字母R(表示余数)。
1700995030
1700995031


1700995032
1700995033
1700995034
之后,将下式中被圈住的两个数字相加,即1+2=3。因此,我们在商的第二位处写上3。
1700995035
1700995036


1700995037
1700995038
1700995039
然后是3 + 3 = 6。
1700995040
1700995041


1700995042
1700995043
1700995044
再然后是6 + 0 = 6。
1700995045
1700995046


1700995047
1700995048
1700995049
最后,我们算出余数为6 + 2 = 8。
1700995050
1700995051


1700995052
1700995053
1700995054
也就是说,12 302 ÷ 9 = 1 366,余数是8。这个办法真是太简单了!下面再举一例,但我会省去某些细节。
1700995055
1700995056
31 415 ÷ 9
1700995057
1700995058
答案唾手可得!
1700995059
1700995060


1700995061
1700995062
1700995063
首位数是3,然后3 + 1 = 4,4 + 4 = 8,8 + 1 = 9,最后9 + 5 = 14。因此,商是3 489,余数为14。由于14 = 9 + 5,所以我们在商上加1,变成3 490,余数是5。
1700995064
1700995065
下面这道题非常简单,但是答案非常优美。验算工作由大家自行完成(笔算或者心算都可以)。