1700995633
为王牌赋予什么点数才能形成价值最大的牌型?
1700995634
1700995635
于是,有意思的问题随之而来。如果按照传统方法判断牌型的价值高低,那么在你拿到像上图这种既可被视为三条又可被视为两对的牌型时,你肯定选择三条,而不愿意选择两对。但是,这样做的结果是:被视为三条的牌型数量超过被视为两对的牌型,两对反而变成一种更少见的牌型。如果我们试图通过提高两对的牌值来解决这个问题,就会导致两对的数量超过三条,同样的问题再次出现。1996年,数学家史蒂夫·加德布斯(Steve Gadbois)发现了这个现象,并得出了一个令人吃惊的结论:如果扑克牌游戏中可以使用王牌,就不可能始终根据牌型概率来决定牌型的价值。
1700995636
1700995637
1700995638
1700995639
1700995640
12堂魔力数学课 [:1700993730]
1700995641
12堂魔力数学课 帕斯卡三角形和圣诞节礼物
1700995642
1700995643
请仔细观察下图中的帕斯卡三角形(Pascal’s triangle):
1700995644
1700995645


1700995646
1700995647
1700995648
用符号表示的帕斯卡三角形
1700995649
1700995650


1700995651


1700995652
我们在本书第1章学过,把数字排列成三角形就会表现出一些有趣的规律。本章讨论的数字排列成三角形时,也会形成非常美丽的规律。这个三角形被称为帕斯卡三角形,如上图所示。利用公式,我们可以把上图中的符号变成数字,如下图所示,然后寻找其中的规律。本章将对大多数规律做出解释,但你在第一遍阅读时尽可以略过不读,只要了解它有哪些规律即可。
1700995653
1700995654


1700995655
1700995656
1700995657
用数字表示的帕斯卡三角形
1700995658
1700995659


1700995660
在用符号表示的帕斯卡三角形中,第0行只有一项,即= 1。(记住,0! = 1。)在用数字表示的帕斯卡三角形中,由于所有行的第一项和最后一项都是1,因此:
1700995661
1700995662


1700995663
1700995664
1700995665
请认真观察第5行:
1700995666
1700995667
第5行:1 5 10 10 5 1
1700995668
1700995669


1700995670
注意,第二项是5。一般而言,第n行的第2项是n。这是有道理的,因为这个数字表示从n个对象中选取1个的方案数量,它的值等于n。还请注意,这个三角形的每一行都对称:从左至右看与从右至左看是一样的。例如,第5行中有:
1700995671
1700995672
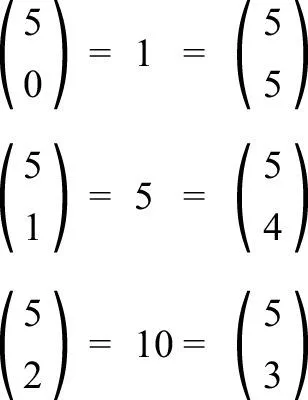
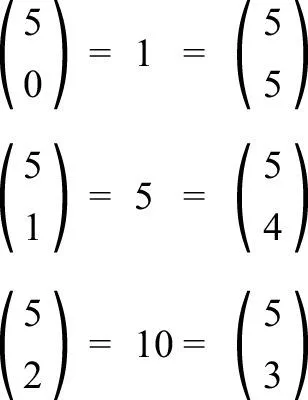
1700995673
1700995674
1700995675
这个规律的一般表达式为:
1700995676
1700995677


1700995678
1700995679
1700995680
延伸阅读
1700995681
1700995682
有两个方法可以证明这种对称关系。根据公式,我们可以进行代数证明: