1700995668
1700995669


1700995670
注意,第二项是5。一般而言,第n行的第2项是n。这是有道理的,因为这个数字表示从n个对象中选取1个的方案数量,它的值等于n。还请注意,这个三角形的每一行都对称:从左至右看与从右至左看是一样的。例如,第5行中有:
1700995671
1700995672
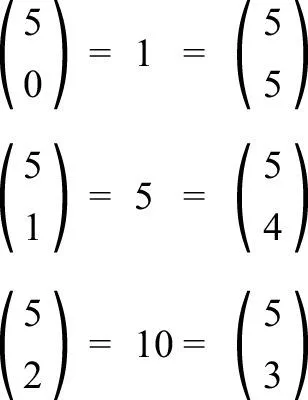
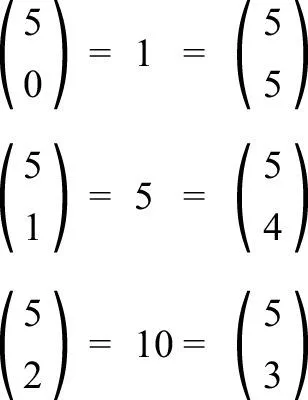
1700995673
1700995674
1700995675
这个规律的一般表达式为:
1700995676
1700995677


1700995678
1700995679
1700995680
延伸阅读
1700995681
1700995682
有两个方法可以证明这种对称关系。根据公式,我们可以进行代数证明:
1700995683
1700995684


1700995685
1700995686
1700995687


1700995688


1700995689


1700995690
但是,无须借助公式,我们也能理解其中的道理。例如,为什么=呢?数字表示(从10种口味的冰激凌中)选择3种口味的冰激凌放到一个杯子里,这同时意味着有7种口味的冰激凌不会被放到杯子里,两者是一回事。
1700995691
1700995692
你也许还看出了另外一个规律:各行中的所有数字,除去开头和结尾的那些1以外,都是其正上方的两个数字之和。我们把这个令人惊讶不已的关系称作“帕斯卡恒等式”(Pascal’s identity)。例如,观察帕斯卡三角形的第9行和第10行:
1700995693
1700995694


1700995695
1700995696
1700995697
每个数字都是其正上方的两数之和
1700995698
1700995699
这是为什么呢?既然120 = 36 + 84,那么换成计数问题,这个等式就变成以下形式:
1700995700
1700995701


1700995702
1700995703
1700995704


1700995705


1700995706


1700995707


1700995708


1700995709
为了理解其中的道理,我们先来思考这个问题:如果一家商店出售10种口味的冰激凌,你要买一个包含3种不同口味的圆筒冰激凌(口味的次序不重要),会有多少种选择呢?第一种答案是我们已经知道的:。但是,我们还可以换一个方法解决这个问题。假设其中一种口味是香草味,那么不含香草味的圆筒冰激凌有多少种呢?答案是,因为我们可以在剩下的9种口味中任意选择3种。含有香草味的圆筒冰激凌有多少种呢?如果香草味是必选口味,那么其余两种口味有种可选方案。因此,一共有+种选择。哪个答案是正确的呢?两个方法的逻辑都正确,因此两个答案都正确,也就是说它们的值是相同的。同理(如果你愿意,也可采用代数方法),对于0~n中的任意数k,下列公式都是成立的:
1700995710
1700995711


1700995712
1700995713
1700995714
接下来,我们把帕斯卡三角形中各行的数字分别相加(如下图所示),观察其中的规律。
1700995715
1700995716


1700995717