打字猴:1.700995744e+09

1700995744

1700995745

1700995746 如果要求所选冰激凌口味各不相同，一共可以制成多少种圆筒呢？圆筒里可以放入1、2、3、4或5种口味的冰激凌，而且先后次序不重要。有2种口味的冰激凌有多少种？前文中说过，有= 10种。根据所选口味的数量，圆筒冰激凌的总数为：

1700995747

1700995748

1700995749

1700995750

1700995751 化简后是1 + 5 + 10 + 10 + 5 + 1。此外，我们也可以用乘法法则来回答这个问题。我们先不考虑圆筒中有几种口味的冰激凌，而是针对每种口味考虑是否把它放进圆筒里。例如，巧克力味的冰激凌有2种选择（放或不放），香草味有2种选择（放或不放），以这种方式考虑全部5种口味的情况。（注意，如果我们针对每种口味所做的选择都是“不放”，最终得到的将是一个空圆筒，但这个结果是允许出现的。）因此，我们一共可以做出的圆筒冰激凌数量是：

1700995752

1700995753 2×2×2×2×2 = 25

1700995754

1700995755 由于两种方法都是合乎逻辑的，因此：

1700995756

1700995757

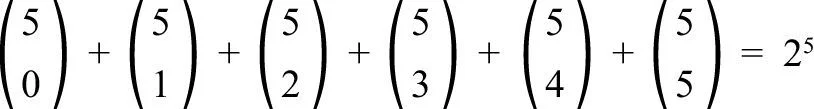
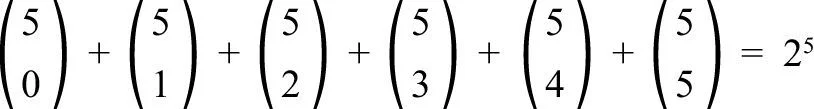
1700995758

1700995759

1700995760 证明完毕。

1700995761

1700995762 延伸阅读

1700995763

1700995764 通过类似的组合证明法可以发现，如果以间隔一个数的方式对第n行求和，得数是2n– 1。对于奇数行而言，这个规律很好理解。以第5行为例，1 + 10 + 5与被排除在外的5 + 10 + 1的得数一样，都等于所有数字之和2n的1/2。对于偶数行而言，这个规律同样有效。以第4行为例，1 + 6 + 1 = 4 + 4 = 23。一般而言，对于任意的n≥1，都有：

1700995765

1700995766

1700995767

1700995768

1700995769 这是为什么呢？等式左边表示圆筒中的冰激凌口味数量是偶数（冰激凌共有n种且口味各不相同）。我们也可以通过在第1至第（n– 1）种口味的冰激凌中做选择的方式配制出这些冰激凌。第1种口味的冰激凌有2个选择（放或不放），第2种口味有2个选择……第（n– 1）种口味有2个选择。但是，要让圆筒中冰激凌的口味数量是偶数，最后一种口味只能有1个选择。因此，冰激凌口味为偶数的圆筒数量是2n– 1。

1700995770

1700995771 把帕斯卡三角形转化成直角三角形的形式，就可以发现更多的规律。最前面的一列（第0列）的各项都是1，紧随其后的一列（第1列）都是1、2、3、4等正整数。第2列的前几项是1、3、6、10、15…大家应该比较熟悉，这些都是我们在第1章里讨论过的三角形数。第2列的各个数字也可以写成:

1700995772

1700995773