1700996607
1700996608
定理:两个有理数的平均数仍然是有理数。
1700996609
1700996610
证明:令x和y为有理数,必然存在a、b、c、d,满足x=a/b,y=c/d。所以,x和y的平均数为:
1700996611
1700996612
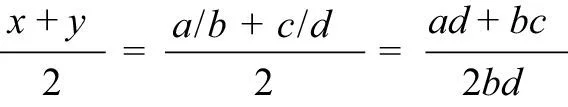
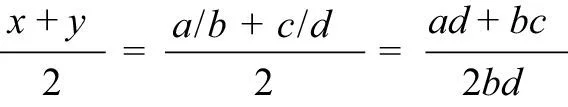
1700996613
1700996614
1700996615
由此可见,该平均数是一个分数,且分子、分母均为整数。因此,有理数x和y的平均数也是有理数。
1700996616
1700996617


1700996618


1700996619


1700996620
我们想一想,这个定理有什么含义?它的意思是,对于任意两个有理数,即使它们非常接近,我们也总能找出一个位于它们之间的有理数。也许你忍不住会想,所有的数字都是有理数(古希腊人也曾有这样的想法)。但是,令人吃惊的是,这个想法是错误的。我们以为例,这个数字的小数形式是1.414 2…。现在,我们有很多方法,用分数来近似地表示。例如,近似等于10 / 7或者1 414 /1 000,但是这些分数的平方都不会正好等于2。是不是因为我们找得还不够仔细呢?下面这个定理告诉我们,无论我们怎么努力,都会无功而返。该定理的证明采用了反证法,关于无理数的定理通常都会采用这种证明方法。我们知道,所有分数都可化简至最简分数,即分子和分母没有大于1的公因数。下面的证明过程就将利用分数的这个特点。
1700996621
1700996622


1700996623
定理:是无理数。
1700996624
1700996625


1700996626
证明:我们假设是有理数,则必然存在正整数a和b,满足:
1700996627
1700996628


1700996629
=a/b
1700996630
1700996631
其中,a/b是最简分数。等式两边同时进行平方运算,就有:
1700996632
1700996633
2 =a2/b2
1700996634
1700996635
也就是说,a2= 2b2。由此可知,a2必然是偶数。如果a2是偶数,那么a也必然是偶数(前文中已经证明,如果a是奇数,那么其自乘的结果也必然是奇数)。因此,a= 2k,k是整数。将它代入上面的等式,就有:
1700996636
1700996637
(2k)2= 2b2
1700996638
1700996639
4k2= 2b2
1700996640
1700996641
b2= 2k2
1700996642
1700996643


1700996644


1700996645


1700996646
因此,b2是偶数。既然b2是偶数,b也必然是偶数。但是,a和b都是偶数,这与a/b是最简分数的前提相矛盾。因此,是有理数这个假设不成立,这证明是无理数。
1700996647
1700996648
单凭逻辑的力量,就证明了一个非常令人吃惊的结果,所以我十分喜欢这个证明过程(画了个笑脸)。本书第12章将告诉我们,无理数非常多。事实上,从严格意义上讲,绝大多数的实数都是无理数,尽管我们在日常生活中接触的大多是有理数。
1700996649
1700996650
上面这条定理有一个有趣的“推论”(corollary),推论是指由某条定理推导得出的定理。这个推论的推导过程利用了“指数定律”(law of exponentiation),即对于任意整数a、b、c:
1700996651
1700996652
(ab)c=abc
1700996653
1700996654
例如,(53)2= 56,这是有道理的,因为:
1700996655
1700996656
(53)2= (5 × 5 × 5) × (5 × 5 × 5) = 56