1701008056
在此模型中假设金箔的损耗包括可能的损耗和其他技术因素,不包括施工过程中,外界的因素致使大量的金箔无法使用等。
1701008057
1701008058
在此,考虑整个球或椭圆球的情形。半径为30米的球与半立轴是30米,半长轴和半短轴分别是30.6米和29.6米的椭圆球如图6-16和图6-17所示。
1701008059
1701008060


1701008061


1701008062
图6-16 清真寺圆顶 图6-17 清真寺椭圆体顶 (1)对于球半盖,其方程为:
1701008063
1701008064


1701008065
1701008066
1701008067
上式变形如下,仅求解上半球的表面积:
1701008068
1701008069
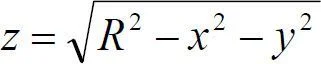
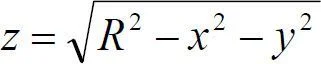
1701008070
1701008071
1701008072
求方程中z对x、y偏导数为:
1701008073
1701008074


1701008075
1701008076
1701008077
则球半盖的表面积积分为:
1701008078
1701008079


1701008080
1701008081
1701008082
当且仅当H=R,S=2πR2=2π×302=5654.9。
1701008083
1701008084
实际用量将会比清真寺顶部面积多1.5%。
1701008085
1701008086


1701008087
1701008088
1701008089
具体的MATLAB程序如下:
1701008090
1701008091
clc,clear,close all %清屏和清除变量 warning off %消除警告 syms x y z R r H z=sqrt(R^2-x^2-y^2); dz_dx=diff(z); dz_dy=diff(z,‘y’); z1=sqrt((dz_dx)^2+(dz_dy)^2+1); z2=R/sqrt(R^2-r^2); z3=z2*r; Intxy=int(int(z3,‘r’,0,‘R’),‘y’,0,2*pi); >> pretty(Intxy) 2 1/2 2 (R ) R pi >> R=30; >> Intxy=2*(R^2)^(1/2)*R*pi Intxy = 5.6549e+003 >> Intxy*1.015 ans = 5.7397e+003
1701008092
1701008093
(2)对于半椭球而言,其方程如下:
1701008094
1701008095


1701008096
1701008097
1701008098
其偏导数为:
1701008099
1701008100


1701008101
1701008102
1701008103
则椭圆球半盖的表面积积分编程如下:
1701008104
1701008105
clc,clear,close all %清屏和清除变量 warning off %消除警告 >> syms x y z a b c >> z=sqrt(c^2*(1-y^2/b^2-x^2/a^2)); >> dz_dx=diff(z,‘x’) dz_dx = -1/(c^2*(1-y^2/b^2-x^2/a^2))^(1/2)*c^2*x/a^2 >> dz_dy=diff(z,‘y’) dz_dy = -1/(c^2*(1-y^2/b^2-x^2/a^2))^(1/2)*c^2*y/b^2 >> z1=sqrt((dz_dx)^2+(dz_dy)^2+1); >> pretty(z1) / 2 2 2 2 \1/2 | c x c y | |––––––— + ––––––— + 1| |/ 2 2 \ / 2 2 \ | || y x | 4 | y x | 4 | ||1 - –- - –-| a |1 - –- - –-| b | || 2 2 | | 2 2 | | \ b a / \ b a / / >> %Intxy=int(int(z1,‘x’,-sqrt(a^2*(1-y^2/b^2)),sqrt(a^2*(1-y^2/b^2))),‘y’,-b,b)