1701023315
1701023316
我要告诉大家一个好消息:到2048年,不会人人都超重。为什么呢?因为不是所有的线都是直线。
1701023317
1701023318
但是,我们在前面讨论过,牛顿发现所有的线都与直线非常接近,由此催生了“线性回归”(linear regression)这个概念。社会学经常要用到线性回归分析这种统计学技术,就像居家维修要使用螺丝刀一样。我们在报纸上看到的那些内容,诸如:有很多亲戚的人会更幸福;“汉堡王”连锁店开得越多的国家,越容易面临道德沦丧的问题;烟酸摄入量减半的话,患足癣的危险就会加倍;收入每增加1万美元,美国人把选票投给共和党的可能性就会增加3%,等等。所有这些,都是线性回归分析的结果。
1701023319
1701023320
下面,我告诉大家线性回归分析的使用方法。假设你要分析两个事物之间的关系,比如大学学费与新生SAT平均分。你可能认为,SAT分数高的学校,很有可能收费也高,但是我们稍做数据分析,就会发现并非如此。毗邻北卡罗来纳州伯灵顿市的伊隆大学,新生数学与语言测试的平均分是1 217分,年均学费是20 441美元。与伊隆大学距离不远、位于格林波若的吉尔佛大学,学费稍高,为23 420美元,但是新生的SAT平均分仅为1 131分。
1701023321
1701023322
如果进一步研究多所学校的情况,比如2007年把学费与SAT分数情况报告给北卡罗来纳职业资源网的31所私立高校,就能清楚地看到某种趋势。
1701023323
1701023324
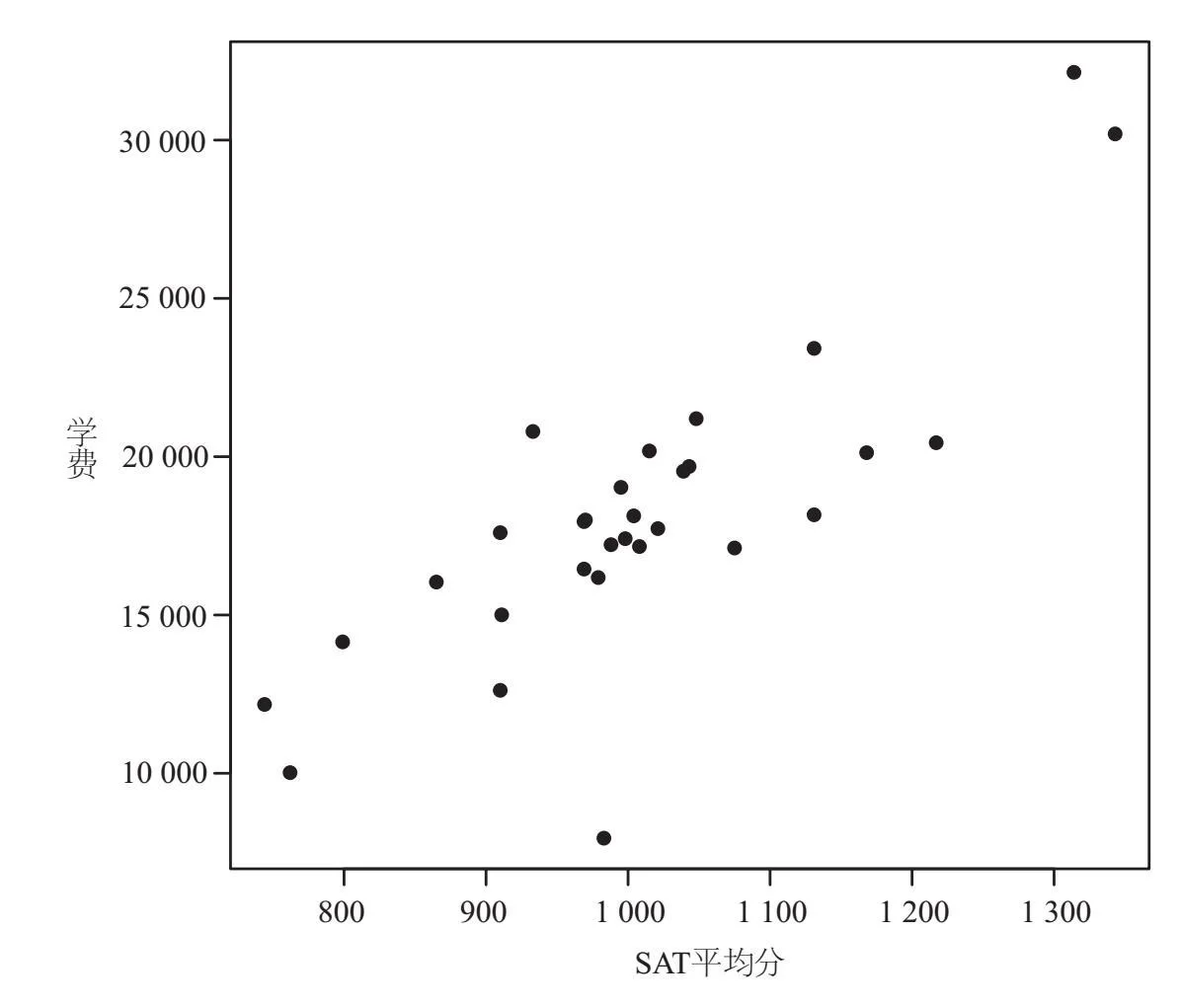
下图中每个点分别代表其中一所高校。靠近右上角的位置有两个点,SAT分数与学费都非常高,代表的是维克森林大学和戴维森学院。靠近底部的位置有一个孤零零的点,代表的是卡巴拉斯健康科学学院,是这些私立高校中唯一一所学费低于1万美元的大学。
1701023325
1701023326

1701023327
1701023328
1701023329
上图表明,总的来说,分数高的学校收费也高。但是,高多少呢?这就需要在图中引入线性回归这个工具了。在上图中,所有的点很明显都不在同一条直线上。但是,这些点并不十分分散,我们可以徒手画出一条直线,从这些点比较集中的位置穿过。借助线性回归,无须猜测,就可以画出最接近于[1]所有点的直线。对于北卡罗来纳的高校,这方面的大致情况可用下图表示。
1701023330
1701023331


1701023332
1701023333
1701023334
图中直线的倾斜角度约为28度,这意味着:如果学费真的完全取决于SAT分数,而且决定关系可由我在图中绘制的直线来表示,那么SAT分数每提高1分,与之相对应,学费就会增加28美元。如果新生的SAT平均分提高50分,就可以把新生的人均学费提高1 400美元。(从学生家长的角度看,孩子的分数提高100分,就意味着家长每年要多支付2 800美元的学费。由此可见,考试辅导班比我们预想的要贵得多!)
1701023335
1701023336
线性回归是一个非常实用的工具,用途广泛、操作简便,只需要在数据表上点击鼠标即可完成。这个工具可以用来处理包含两个变量的数据集(就像前文中我绘制的那些图),而且,在处理含有三个变量甚至1 000个变量的数据集时,效果同样好。在希望了解哪些变量对其他变量有作用以及作用方向时,我们第一个想到的就是线性回归。不夸张地说,线性回归可以处理所有数据集。
1701023337
1701023338
线性回归应用广泛,这既是一个长处,也会带来问题。我们尚未考虑正在建模的现象是否真的接近于线性,就可能会迫不及待地对其进行线性回归,但这样做肯定是不妥当的。的确,我说过,线性回归就像一把螺丝刀,但是从另一个方面看,它更像一把锯。如果未经考虑拿来就用,那么后果可能会相当可怕。
1701023339
1701023340
以上一章讨论的导弹发射为例。也许,导弹根本不是我们发射的,甚至有可能我们就是导弹要袭击的目标。因此,我们迫切希望尽可能准确地分析导弹的运动轨迹。
1701023341
1701023342
如果我们已经把导弹在不同时间点上的竖直位置绘制成5个点,那么这幅图大概如下图所示:
1701023343
1701023344


1701023345
1701023346
1701023347
接着,我们迅速完成了线性回归并得出了完美的分析结果。我们画出的直线几乎正好从那5个点上穿过:
1701023348
1701023349


1701023350
1701023351
1701023352
(一旦完成上述操作,就代表我们的手正在伸向锯子锋利的锯齿。)
1701023353
1701023354
这条直线为导弹的运动轨迹建立了一个精准的模型:在飞行过程中,导弹每分钟都会升高固定的高度,比如说400米。一小时之后,导弹会飞升到距离地面24 000米的高度。那么,导弹何时落地呢?根本不会落地!这条直线将一直向上延伸,这就是直线的特点。
1701023355
1701023356
(血花飞溅,皮开肉绽,凄厉的惨叫声。)
1701023357
1701023358
不是所有的线都是直线,所以导弹的运动轨迹绝对不可能是直线,而是抛物线。就像阿基米德的圆一样,近距离观察这条抛物线,就像一条直线。正因为如此,在跟踪到导弹之后,线性回归可以成功地告诉我们5秒之后该导弹所在的位置。但是,如果间隔了一个小时呢?想都别想!我们根据模型预测导弹会处于平流层下层,而实际上导弹可能就要落到我们的屋顶上了。
1701023359
1701023360
针对这种不假思索就进行线性回归的最生动警告,不是统计学家发出的,而是来自马克·吐温(Mark Twain)。他在小说《密西西比河上的生活》(Life on the Mississippi)[2]中写道:
1701023361
1701023362
176年前,密西西比河在凯罗与新奥尔良之间的河段长1 215英里[3]。经过1722年的截弯取直之后,这个河段缩短为1 180英里,之后在美洲湾取直之后,缩短为1 040英里。再后来,这个河段又缩短了67英里,因此,现在它的长度仅为973英里……在176年的时间里,下密西西比河缩短了31英里多。因此,只要不是瞎子和白痴,稍做冷242英里,平均每年缩短1静的分析,我们就不难推测出,在距明年11月有100万年间隔的鲕状岩志留纪时期(Old Oolitic Silurian Period),下密西西比河应该有130万英里长,像一根钓鱼竿一样,远远地伸出墨西哥湾。同样,我们也会推测出,再过742年,下密西西比河将只有131英里长。到那时,凯罗与新奥尔良会连成一片,那里的人们在同一位市长与同一个市政委员会的领导下,勤勤恳恳地过着舒舒服服的日子。这就是科学的魅力,只要对事实稍加调查,我们就能生出无数的猜想。
1701023363
1701023364
学生应该从数学课上学些什么?