1701044741
1701044742
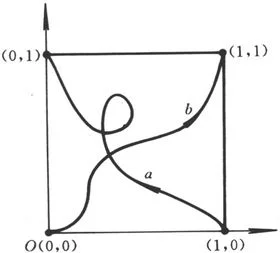
6.把三角形的三条边按图4-30所示方式粘接在一起.求所得商空间的基本群.
1701044743
1701044744
7.证明:如果曲面M与N同胚,则它们的边界也同胚.并由此说明Möbius带与平环不同胚.
1701044745
1701044746


1701044747
1701044748
1701044749
图4-30
1701044750
1701044751
8.设f:D2→E2连续.证明在下列条件之一成立时,f有不动点:
1701044752
1701044753
(1)f(S1)⊂D2;
1701044754
1701044755
(2)∀x∈S1,f(x),x与原点不共线;
1701044756
1701044757


1701044758
(3)∀x∈S1,线段过原点.
1701044759
1701044760
9.设f:D2→D2连续,并且S1上每一点都不动,证明f是映满的.
1701044761
1701044762


1701044763


1701044764


1701044765


1701044766
10.记是E3中以(i,0,0)为球心,为半径的球面,(图4-31).证明X单连通.
1701044767
1701044768


1701044769
1701044770
1701044771
图4-31
1701044772
1701044773
基础拓扑学讲义 [:1701040222]
1701044774
*§6 Jordan曲线定理
1701044775
1701044776
平面或球面上同胚于圆周S1的子集称为Jordan曲线,或称为简单闭曲线.
1701044777
1701044778
定理4.10(Jordan曲线定理) 若J是E2上的一条Jordan曲线,则E2\J有两个连通分支,它们都以J为边界.
1701044779
1701044780
这是一个应用十分广泛的著名定理.它看起来很直观,而证明起来很困难,但迄今已有不少证法.下面用基本群为工具给出一个证明.
1701044781
1701044782
先指出几个明显事实.
1701044783
1701044784
(1)E2\J是E2的开集,因此是曲面,并且没有边界点.它局部道路连通,从而连通分支就是道路分支,并且都是E2中的开集.
1701044785
1701044786
(2)E2\J有唯一无界连通分支.
1701044787
1701044788

1701044789
1701044790