1701044805


1701044806


1701044807


1701044808


1701044809


1701044810
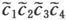
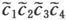
1701044811


1701044812


1701044813
则f(0,0)=1,记m1,m2,m3和m4分别是S1上在四个象限中的弧(图4-33).记I×I四条边决定的道路为和如图中所标,则不难发现,的像在mi上.由此可看出是S1以1为基点的闭路,圈数为1.但是是I×I中的闭路,因此是π1(S1)的单位元,矛盾. ▎
1701044814
1701044815


1701044816
1701044817
1701044818
图4-33
1701044819
1701044820
定理4.10的证明 证明分三步进行.
1701044821
1701044822
第一步 证明E2\J不道路连通.
1701044823
1701044824


1701044825


1701044826


1701044827


1701044828


1701044829


1701044830
取J上距离最大的两点A,B(即d(A,B)=diamJ).作矩形M,使得A,B恰好是它一双对边的中点,并且J包含在M中,只有A,B两点在M的边界上(图4-34).把J被A,B分割成的两段分别记作J1和J2,它们都同胚于I,从而可看作M上从A到B的两条道路的像.根据引理,若C和D是M的上、下边的中点,则线段与J1和J2都相交.记P1是与J的最高交点,P2是最低交点.不妨设P1∈J1,则P2∈J2(否则可设计从C到D的M中一条道路如下:从C直下到P1,沿J1从P1到P2,再从P2直下到D,这条道路与J2无交点).记P4是与J2的最高交点,P3是与J1的最低交点,则的内部无J上的点.取Q为的一内点.下面用反证法证明在E2\J中,Q与M外的部分不在同一分支中.如果有道路a与J不相交,且a(0)=Q,a(1)在M外,则a与M的边界必相交.设第一个交点是E点,则E不是A,B,设E在边界上半部分.构造M中从D到C的道路如下:从D直上P2,沿J2从P2到P4,直上到Q,沿a到E,再沿M的边界的上半部分从E到C.这是一条与J1不相交的道路,与引理的结论相矛盾.
1701044831
1701044832


1701044833
1701044834
1701044835
图4-34
1701044836
1701044837
第二步 证明E2\J的每个连通分支都以J为边界.
1701044838
1701044839


1701044840


1701044841


1701044842


1701044843
对于E2\J的一个有界连通分支U,记就是U的边界.因为E2\J的每个连通分支都是开集,它们都与不相交,从而与∂U不相交,于是∂U⊂J.下面用反证法证∂U=J.如果∂U≠J,则由于∂U是J的闭子集,一定存在J的一闭弧使得∂U⊂L.利用Tietze扩张定理,对于E2的闭集L,id:L→L可扩张为收缩映射r:E2→L.构造连续映射f:E2→E2如下:
1701044844
1701044845


1701044846
1701044847
1701044848


1701044849


1701044850


1701044851


1701044852
其中i:L→E2是包含映射(注意到当时,ir(x)=x,这说明f的合理性).是有界的,不妨设它在D2的内部.于是由f在D2上的限制得到D2的自映射f0:D2→D2,它在S1上不动,并且f0不满(因为U⊂D2,而且∀x,这与§5习题9的结果矛盾.
1701044853
1701044854
对于无界分支U,证法相同,只须把f的定义修改为: