1701045688
1701045689
首先,低维单纯形都是各自顶点集的凸包,即包含它的各顶点的最小凸集,从而它们由顶点完全确定.其次,这些低维单纯形的顶点是要满足一定的几何条件的,如三角形的三个顶点不共线,四面体的顶点不共面等.这些条件推广为下面的概念:欧氏空间中的有限点集A={a0,a1,…,an}称为处于一般位置(或称几何无关),如果对于它们,满足下列两个条件:
1701045690
1701045691


1701045692
(1)
1701045693
1701045694


1701045695
(2)
1701045696
1701045697
的实数组λ0,λ1,…,λn一定都为0.
1701045698
1701045699
显然当A只有一点时,它是处于一般位置的,两个不同点也处于一般位置.从解析几何知道,当n=2或3时,A处于一般位置相当于它不共线或不共面.下面的命题给出点组处于一般位置与向量组线性无关这两个概念的联系.
1701045700
1701045701


1701045702
命题6.1 设n>0,则A={a0,…,an}处于一般位置向量组{a1-a0,…,an-a0}线性无关.
1701045703
1701045704


1701045705


1701045706


1701045707


1701045708
证明 .设实数组λ1,…,λn使得记则并且
1701045709
1701045710
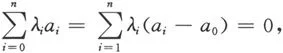
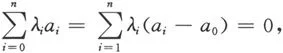
1701045711
1701045712
1701045713
由A处于一般位置得到λ1=λ2=…=λn=0,因此{a1-a0,…,an-a0}线性无关.
1701045714
1701045715


1701045716


1701045717


1701045718
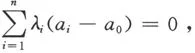
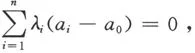
1701045719
.设实数组λ0,λ1,…,λn符合(1)和(2),从(1)得出代入(2)得到由于{a1-a0,…,an-a0}线性无关,得到λ1=…=λn=0,再从(1)得出λ0=0,这说明A处于一般位置. ▎
1701045720
1701045721
如果a0用任何别的ai代替,命题仍然成立.
1701045722
1701045723
定义6.1 欧氏空间中处于一般位置的n+1个点{a0,…,an}(n≥0)的凸包称为一个n维单纯形,简称n维单形,记作(a0,a1,…,an).称ai为它的顶点,i=0,…,n.
1701045724
1701045725


1701045726


1701045727
本书中为了简便,常用小写英文字母或希腊字母来命名一个单形,并在下面加一横线,如单形单形>等.0维单形只有一个点,即它唯一的顶点a,通常就记作a.
1701045728
1701045729
不难验证,对于欧氏空间的任一子集A,A的凸包为
1701045730
1701045731


1701045732


1701045733
只有有限个不为0,并且
1701045734
1701045735
因此作为点集,
1701045736
1701045737

