1701047702
下面都是映射度的应用.作为映射度的直接应用,首先来完成Brouwer不动点定理的证明.
1701047703
1701047704
第四章中已叙述了Brouwer不动点定理,并把它的证明归结到证明Sn-1上恒同映射不零伦.综合命题8.1的(3)与(4),直接得到这个断言,从而完成了Brouwer定理的证明.
1701047705
1701047706
1.2 对径映射的映射度及其应用
1701047707
1701047708
球面Sn看作En+1中的单位球面,Sn的对径映射即Sn关于原点O的中心对称,记作h∶Sn→Sn.于是h(x)=-x,∀x∈Sn.
1701047709
1701047710
显然h2=id,因此
1701047711
1701047712
(deg(h))2=deg(id)=1,
1701047713
1701047714
从而
1701047715
1701047716
|deg(h)|=1.
1701047717
1701047718
剩下要决定deg(h)的正负性.
1701047719
1701047720
命题8.2 设h∶Sn→Sn是对径映射,则
1701047721
1701047722
deg(h)=(-1)n+1.
1701047723
1701047724
证明 作复形Σn如下.
1701047725
1701047726
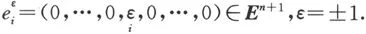
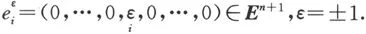
1701047727
记规定
1701047728
1701047729


1701047730
1701047731
1701047732


1701047733
1701047734
1701047735
图8-1
1701047736
1701047737
图8-1中画出了Σ2,它是正八面体的边界.
1701047738
1701047739


1701047740


1701047741
我们不难看出它也是关于原点O中心对称的.记r∶|Σn|→Sn为中心投影,即由规定的映射,则r是同胚,从而(Σn,r)是Sn的剖分.
1701047742
1701047743


1701047744


1701047745


1701047746


1701047747


1701047748
记h′=r-1hr∶|Σn|→|Σn|,则h′是|Σn|上的中心对称映射.记φ∶Σn→Σn是由顶点对应决定的单纯映射,则因此φ就是h′的单纯逼近.约定
1701047749
1701047750
取zn∈Cn(Σn)为
1701047751