1701047724
证明 作复形Σn如下.
1701047725
1701047726
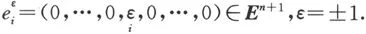
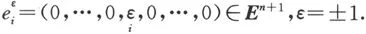
1701047727
记规定
1701047728
1701047729


1701047730
1701047731
1701047732


1701047733
1701047734
1701047735
图8-1
1701047736
1701047737
图8-1中画出了Σ2,它是正八面体的边界.
1701047738
1701047739


1701047740


1701047741
我们不难看出它也是关于原点O中心对称的.记r∶|Σn|→Sn为中心投影,即由规定的映射,则r是同胚,从而(Σn,r)是Sn的剖分.
1701047742
1701047743


1701047744


1701047745


1701047746


1701047747


1701047748
记h′=r-1hr∶|Σn|→|Σn|,则h′是|Σn|上的中心对称映射.记φ∶Σn→Σn是由顶点对应决定的单纯映射,则因此φ就是h′的单纯逼近.约定
1701047749
1701047750
取zn∈Cn(Σn)为
1701047751
1701047752


1701047753
1701047754
1701047755
容易验证∂nzn=0,即zn∈Zn(Σn)=Hn(Σn).zn≠0,并且
1701047756
1701047757


1701047758
1701047759
1701047760
按定义,deg(h)=(-1)n+1. ▎
1701047761
1701047762


1701047763
如果n是正偶数,则deg(h)=-1,从而
1701047764
1701047765
定理8.1 设n是正偶数,p∶Sn→X是复叠映射,则p是2叶复叠映射或同胚映射.
1701047766
1701047767


1701047768


1701047769
证明 因为Sn单连通,p是泛复叠映射,所以p的叶数就是复叠变换群(Sn,p)中元素的个数,要证#(Sn,p)≤2.
1701047770
1701047771


1701047772


1701047773
如果g∈(Sn,p),g不是id∶Sn→Sn,则g无不动点,即g(x)≠x=-h(x).于是(第四章§1例2),从而deg(g)=deg(h)=(-1)n+1=-1.