1701047865


1701047866


1701047867
证明 用单纯逼近的方法证明,沿用命题8.2的证明中规定的Σn,h′,r等记号.记f′=r-1fr∶|Σn|→|Σn|,则f′也是对径的,即f′h′=h′f′.取足够大的自然数q,使得f′关于L=(Σn)(q)和Σn有星形性质.L也是关于原点O中心对称的复形,因此∀a∈L0,StL(-a)=h′(StLa).于是当b∈(Σn)0使得时,这样,可构作f′的单纯逼近ψ∶L→Σn,使得∀a∈L0,ψ(-a)=-ψ(a),从而也是保径的.令不难验证g满足引理的要求. ▎
1701047868
1701047869
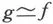
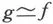
1701047870
引理2 若f∶Sn→Sn是保径映射,则存在保径映射g,满足,并且g(Sn-1)⊂Sn-1.
1701047871
1701047872


1701047873


1701047874


1701047875
证明 由引理1,不妨假定f(Sn-1)≠Sn,并且和不在f(Sn-1)中.规定为:
1701047876
1701047877


1701047878
1701047879
1701047880


1701047881
记g0=jf|Sn-1∶Sn-1→Sn.则g0(Sn-1)⊂Sn-1,并且不难看出g0保径地同伦于f|Sn-1,即存在从f|Sn-1到g0的同伦H0,使得
1701047882
1701047883
H0(-P,t)=-H0(P,t), ∀P∈Sn-1,t∈I.
1701047884
1701047885


1701047886


1701047887


1701047888


1701047889


1701047890
记是上半球面,即则X是×I的形变收缩核.取为一个收缩映射.规定G0∶X→Sn为
1701047891
1701047892


1701047893
1701047894
1701047895


1701047896


1701047897
记并规定为
1701047898
1701047899


1701047900
H_(P,t)=-H+(-P,t),t∈I.
1701047901
1701047902


1701047903


1701047904
于是在和的交集Sn-1×I上,H-和H+的限制都是H0,从而可粘接H+和H-得到同伦H∶Sn×I→Sn,它是H0的扩张,并且H(P,0)=f(P),∀P∈Sn.规定g为g(P)=H(P,1),∀P∈Sn.不难验证g满足引理的要求. ▎
1701047905
1701047906
作Σn的n-1维闭链
1701047907
1701047908


1701047909
1701047910
1701047911
它在Σn-1中,是Zn-1(Σn-1)的生成元.规定Σn的n维链
1701047912
1701047913


1701047914