1701048247
1701048248
设A是自由交换群F的基,H是一交换群,则从A到H的任一对应θ∶A→H可按下式唯一决定同态φ∶F→H,
1701048249
1701048250


1701048251
1701048252
1701048253
称φ是θ的线性扩张.
1701048254
1701048255
定义A.2 如果交换群H有一有限子集
1701048256
1701048257
A={a1,a2,…,ar},
1701048258
1701048259
使得H的每个元素x可表成
1701048260
1701048261
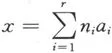
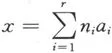
1701048262
1701048263
1701048264
的形式,则称H是有限生成交换群,称A是它们的一个生成元组.
1701048265
1701048266


1701048267
命题A.1 交换群H是有限生成的H是一个有限基自由交换群的商群.
1701048268
1701048269


1701048270
证明 .设j∶F→H是满同态,其中F是有限基自由群.设{f1,f2,…,fr}是F的基,则显然{j(f1),…,j(fr)}是H的生成元组.
1701048271
1701048272


1701048273
.取H的生成元组{a1,a2,…,ar}.构作F为
1701048274
1701048275
F={(n1,…,nr)|ni∈Z},
1701048276
1701048277


1701048278
则F在向量加法下是有限基自由交换群.规定对应j∶F→H为则j是满同态. ▎
1701048279
1701048280
推论 有限生成交换群的商群也是有限生成的. ▎
1701048281
1701048282
根据本书的需要,从现在起,我们只讨论有限生成的交换群.
1701048283
1701048284
设H是有限生成交换群,h∈H称为有限阶的,如果存在r∈N,使得rh=0.记TH是H的全部有限阶元素构成的集合,则TH是H的子群,称为H的挠子群.
1701048285
1701048286
设H0是H的子群,规定
1701048287
1701048288
C(H0)∶={h∈H|存在r∈N,使得rh∈H0}.
1701048289
1701048290
它是H的一个子群.特别地,C(TH)=C(0)=TH.
1701048291
1701048292
命题A.2 (1)H/C(H0)无有限阶非0元素;
1701048293
1701048294
(2)C(H0)/H0的每个元素都是有限阶的.
1701048295
1701048296
证明 (1)设h∈H,使得它代表的商群元素〈h〉∈H/C(H0)是有限阶的,则有r∈N,使得r〈h〉=0,即rh∈C(H0).由定义,存在r′∈N,使得r′(rh)∈H0,于是h∈C(H0),〈h〉=0.