1701050025
1701050026


1701050027
于是平凡.
1701050028
1701050029
4.(1)同构于Z*Z*Z;
1701050030
1701050031
(2)同构于Z*Z;
1701050032
1701050033
(3)同构Z*Z*Z*Z.
1701050034
1701050035
5.(1)同构于Z*Z;
1701050036
1701050037
(2)同构于Z*Z*Z*Z*Z;
1701050038
1701050039
(3)同构于Z*Z*Z*Z.
1701050040
1701050041
6.同构于Z3=Z/3Z.
1701050042
1701050043
8.(1)作收缩映射r∶E2→D2为
1701050044
1701050045


1701050046
1701050047
1701050048


1701050049


1701050050
则rf∶D2→D2有不动点,不难验证当rf(x)=x时,f(x)=x.
1701050051
1701050052


1701050053
(2)作r如(1),则rf有不动点,且不动点不在S1上,从而也必是f的不动点.
1701050054
1701050055
(3)用反证法.若f无不动点,则可作g∶D2→S1为
1701050056
1701050057


1701050058
1701050059
1701050060


1701050061


1701050062
则g连续,且于是零伦,矛盾.
1701050063
1701050064
((1)和(2)也可用(3)的方法证.)
1701050065
1701050066
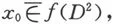
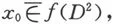
1701050067


1701050068


1701050069
9.用反证法.如果存在则于是D2{x0}以S1为收缩核.记r为一收缩映射,则rf∶D2→S1是收缩映射.这与S1不单连通相矛盾.
1701050070
1701050071
10.方法一 记X1是X中第3个坐标不小于0的点的集合,X2是第3个坐标不大于0的点的集合.则X=X1∪X2,X1,X2都单连通,并且X1∩X2道路连通.用Van-Kampen定理,得X单连通.
1701050072
1701050073


1701050074
方法二 用Van-Kampen定理不难得到下面结论:对任何两个整数单连通.