1701050147
3.因为π1(S2)平凡,f总可提升为零伦,从而f也零伦.
1701050148
1701050149


1701050150
4.同上题.因为π1(T2)是自由群,π1(P2)到π1(T2)的同态只有平凡同态.
1701050151
1701050152
5.按照定义验证.
1701050153
1701050154


1701050155


1701050156


1701050157
∀e∈E2,记b=p2(e).取p2∶E2→B的含b点的道路连通的基本邻域U.记V是中包含e点的分支,则p2|V∶V→U是同胚.不难证明的每个分支Wα或者h(Wα)⊂V,或者h(Wα)∩V=∅,并且h-1(V)就是满足h(Wα)⊂V的那些Wα之并.对每个这样的Wα,(p2|V)(h|Wα)=p1|Wα∶Wα→U是同胚,其中p2|V也是同胚,从而h|Wα∶Wα→V是同胚.这说明h是复叠映射.
1701050158
1701050159
§3
1701050160
1701050161
1.只要证B的每个道路连通的基本邻域U是半单连通的.
1701050162
1701050163


1701050164
1701050165
1701050166
取p-1(U)的一个分支V,则
1701050167
1701050168


1701050169
iπ(π1(U))=iπ(p|V)π(π1(V))
1701050170
1701050171


1701050172
=pπiπ(π1(E))=1.
1701050173
1701050174
因此iπ是平凡的,即U在B中半单连通.
1701050175
1701050176


1701050177
2.当p|q-q′时从而相应的f(见例2)一样.
1701050178
1701050179


1701050180
4.取B的一个道路连通的基本邻域U.则p-1(U)的所有分支在之下映成E1的互不相交的开集{Vα}.并且不难验证
1701050181
1701050182
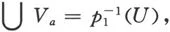
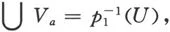
1701050183
(1)且p1|Vα∶Va→U是同胚.从而p1是复叠映射.
1701050184
1701050185


1701050186


1701050187


1701050188
(2)对每个V是p-1(U)中的部分分支之并集,它们每个都被同胚地映射到Vα.由此容易推出也是复叠映射.
1701050189
1701050190


1701050191


1701050192
(用上节第5题也可从p1是复叠映射推出也是复叠映射,因为是从p到p1的同态.)
1701050193
1701050194


1701050195


1701050196

