1701050288
设c2∈C2(K),c2≠0.设c2在2维定向单形s1,s2,…,sn上取不为0的值,在别的2维定向单形上的值为0.记L是由及它们的全部面构成的K的子复形.并设在L的边上.则有的1维顺向面t,它不是s2,…,sn的面.于是∂c2(t)=c2(s1)≠0.从而∂C2≠0.因为L是子复形,c2在K上的边缘链与在L上的边缘链相同,所以这样Z2(K)=0.
1701050289
1701050290
§3
1701050291
1701050292
2.只用证q=1的情形,其余情形由第1题得到.
1701050293
1701050294
显然C1(K)=C1(K1)⊕C2(K2),Z1(K1)⊕Z2(K2)⊂Z1(K).设z1∈Z1(K),且z1=c1+c2,ci∈C1(Ki)(i=1,2).于是,∂c1+∂c2=0.而∂c1=-∂c2在K0=a0中,它必为na0.又从指数的意义知n=0.于是∂c1=∂c2=0,ci∈Z1(Ki)(i=1,2).于是Z1(K)=Z1(K1)⊕Z2(K2).作商群得到结论.
1701050295
1701050296
3.(1)设z=c1+c2,ci∈C1(Ki)(i=1,2).则∂c1+∂c2=0.而∂c1=-∂c2是K0中指数为0的0维链,从而由K0的连通性得知存在K0的一个1维链c3使得∂c3=∂c1.记z1=c1-c3,z2=c2+c3,则∂zi=0,且z=z1+z2.
1701050297
1701050298
(2)证法类似(1).
1701050299
1701050300
(3)设c∈Cq+1(K),∂c=z1+z2.记c=c1+c2,ci∈Cq+1(Ki)(i=1,2).则∂c1+∂c2=z1+z2,从而∂c1-z1=-∂c2+z2是K0中的闭链.由于Hq(K0)=0,∂ci-zi∈Bq(Ki),从而zi∈Bq(Ki)(i=1,2).
1701050301
1701050302
4.利用上题的结果.
1701050303
1701050304
§4
1701050305
1701050306
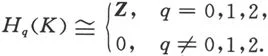
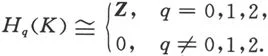
1701050307
2.
1701050308
1701050309


1701050310
3.
1701050311
1701050312
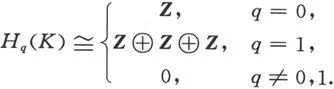
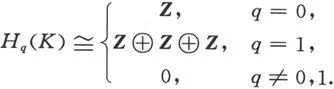
1701050313
4.
1701050314
1701050315


1701050316
6.
1701050317
1701050318


1701050319
7.当q≠0时,Hq(K;G)=0.
1701050320
1701050321
第 七 章
1701050322
1701050323
§1
1701050324
1701050325


1701050326


1701050327
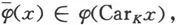
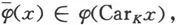
1701050328
3.设Carkx=(a0,a1,…,aq),则λi>0,∀i=0,1,…,q.根据的定义,并且
1701050329
1701050330


1701050331
1701050332
1701050333


1701050334
于是在φ(Carkx)的重心坐标全大于0,从而
1701050335
1701050336


1701050337