1701050297
1701050298
(2)证法类似(1).
1701050299
1701050300
(3)设c∈Cq+1(K),∂c=z1+z2.记c=c1+c2,ci∈Cq+1(Ki)(i=1,2).则∂c1+∂c2=z1+z2,从而∂c1-z1=-∂c2+z2是K0中的闭链.由于Hq(K0)=0,∂ci-zi∈Bq(Ki),从而zi∈Bq(Ki)(i=1,2).
1701050301
1701050302
4.利用上题的结果.
1701050303
1701050304
§4
1701050305
1701050306
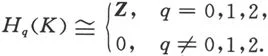
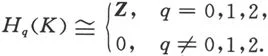
1701050307
2.
1701050308
1701050309


1701050310
3.
1701050311
1701050312
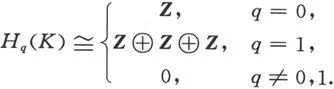
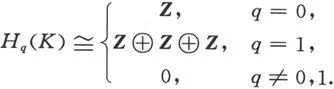
1701050313
4.
1701050314
1701050315


1701050316
6.
1701050317
1701050318


1701050319
7.当q≠0时,Hq(K;G)=0.
1701050320
1701050321
第 七 章
1701050322
1701050323
§1
1701050324
1701050325


1701050326


1701050327
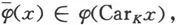
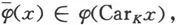
1701050328
3.设Carkx=(a0,a1,…,aq),则λi>0,∀i=0,1,…,q.根据的定义,并且
1701050329
1701050330


1701050331
1701050332
1701050333


1701050334
于是在φ(Carkx)的重心坐标全大于0,从而
1701050335
1701050336


1701050337
1701050338
1701050339


1701050340
5..显然.
1701050341
1701050342


1701050343


1701050344


1701050345
.规定φ∶K→L如下:规定是L中由φ0(a0),…,φ0(aq)所张的单形.不难验证φ是一个单纯映射,并且它的顶点映射就是φ0.
1701050346