1701050374
4.分别记只须证|K|到|L|的任何连续映射都零伦.设f∶|K|→|L|连续,则存在单纯逼近不满,从而零伦,于是也零伦.
1701050375
1701050376


1701050377


1701050378
5.不妨设X,Y都是多面体,且X=|K|,Y=|L|.对任意非负整数r,从K(r)到L的单纯映射是有限个.而每个连续映射f∶X→Y都同伦于一个单纯映射φ∶K(r)→L导出的连续映射由此不难得到结论.
1701050379
1701050380
§3
1701050381
1701050382


1701050383
1.
1701050384
1701050385
2.例如X=S2∨S3∨P2.
1701050386
1701050387


1701050388


1701050389


1701050390
3.X=S2∨S1∨S1.而因而
1701050391
1701050392
§4
1701050393
1701050394
1.因为f零伦.
1701050395
1701050396


1701050397
2.
1701050398
1701050399


1701050400
3.
1701050401
1701050402


1701050403
4.
1701050404
1701050405

1701050406
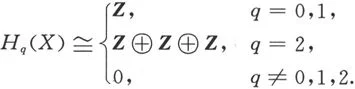
5.
1701050407
1701050408
第 八 章
1701050409
1701050410
§1
1701050411
1701050412
1.如果Sn-1是Dn的收缩核,则包含映射i∶Sn-1→Dn诱导的各维同调群的同态都是单的.但显然i*(n-1)∶Hn-1(Sn-1)→Hn-1(Dn)不是单的.
1701050413
1701050414
2.见第四章§5的习题8的解答.
1701050415
1701050416


1701050417


1701050418
3.设X=f(Dn),则并且f-1∶X→Dn与包含映射i∶Dn→X的复合映射if-1∶X→X一定有不动点,它也就是f的不动点.
1701050419
1701050420
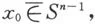
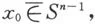
1701050421


1701050422
4.如果f不满,设x0∈Dnf(Dn),则否则f0零伦,从而deg(f0)=0.于是有收缩映射r∶Dn{x0}→Sn-1.于是f0=r(f|Sn-1).由此不难得出(f0)*(n-1)是平凡的,从而deg(f0)=0.
1701050423