1701098510
迄宋代,大将杨承信(921~964年)与弓箭制作使魏丕曾以弹性定律改造弓弩。宋代江少虞辑《宋朝事实类苑》卷十四、《宋史·魏丕传》对此都有文字记载。
1701098511
1701098512
七、横梁高宽比
1701098513
1701098514
中国具有木构建筑的传统。选择一根好的横梁木,是建造新屋的大事。如何选取抗弯曲、抗断裂的木材作为横梁,又是材料力学的内容之一。
1701098515
1701098516
在早期人类建房中,必定有人认为以一根整圆木作梁是坚固耐用的。大概经过几百年、上千年的摸索,才发现矩形木材比圆木更结实。又过了许多年月,才知道矩形木的高宽比例要适当,才能作为梁木使用,又不致浪费材料。
1701098517
1701098518
《国语·周语》中,有“不厚其栋,不能任重”一语。“栋”即梁木,“厚”指其高度。梁木的“厚”要比其宽大,才能承载巨大负荷。《易经·大过》这一卦的卦词以“栋桡”(向下桡)或“栋隆”(向上桡)比喻该卦是凶还是吉。它解释说“栋桡,本末弱也”。“栋桡,凶。象曰,栋桡之凶,不可以有辅也”;“栋隆,吉。有它吝。象曰:栋隆之吉,不桡乎下也”。这正是基础材料力学知识在《易经》占卜中的运用。
1701098519
1701098520
《九章算术·勾股》第4问,是一道从圆木截出矩形木的算题。它得出矩形木的高宽比为:高∶宽=3.43∶1。这种梁木显得高瘦,抗弯有余,材料浪费太多。这大概是汉唐间木工的保守经验的总结。
1701098521
1701098522
北宋时,将作监李诫(?~1110年)主持京城和皇宫建筑。为节约材料和统一发放材料,统一管理,他规定了房屋各种构件的大小尺寸或比例,编修建筑名著《营造法式》一书。在该书中,他确定梁木大小为:“凡梁之大小,各随其广分为三分,以二分为其厚”。这里的“广”与“厚”是对梁木稳定置于地面上(即平放)而言。若将其架在屋架上(即竖放)作架,其“广”就是本书所言的“高”,“厚”是本书所言的“宽”。因此,这种梁木的高(a)宽(b)比为:
1701098523
1701098524


1701098525
1701098526
1701098527
这是一个非常科学的比例数字(如图1.1所示)。
1701098528
1701098529


1701098530
1701098531
1701098532


1701098533


1701098534
西方是砖石结构的建筑传统。因此,直到达·芬奇(L. Da Vinci, 1452~1519年)时,才进行初步的梁木承重实验。伽利略在《两门新科学对话》中作了矩形木平放与竖放的承重实验,得到竖放时材料强度大的结论。但他未进一步取得一个合理的比数。1702年,法国数学家和物理学家帕朗特(A.Parent,1666~1716年)讨论了从圆木中截取最大强度矩形梁的方法(如图1.2所示),结论是:梁断面高宽比应为。这个比数相当于2.8∶2。又一个多世纪后,英国物理学家托马斯·杨(Thomas Young,1773~1829年)在1807年证实,刚性最大的梁,其高宽比为。这个比数相当于3.46∶2。李诫的比数在这两者之间,既考虑材料的强度,又照顾到它的刚度。
1701098535
1701098536


1701098537
帕朗特从圆木中截取最大强度矩形梁的方法是:将圆木直径AB分为三等分,在等分点E、F上分别对直径两侧作垂线、交圆于C、D,矩形ABCD即要截取的梁,如图1.2所示。图中,是个中学几何题,读者不妨去试作证明。
1701098538
1701098539


1701098540
1701098541
1701098542
八、水箱放水实验
1701098543
1701098544
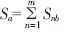
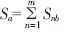
1701098545
水箱放水实验是这样进行的:两个完全相同的等容水箱A与B,盛满同质等高h的水;一个水箱底部开一大孔Sa,另一个底部开数小孔Sab,令数小孔面积之和等于大孔面积,即
1701098546
1701098547
同时打开箱A与B的孔,问哪个水箱内的水先放完(如图1.3所示)?
1701098548
1701098549


1701098550
1701098551
1701098552
这个实验最早是明代徐有贞(1407~1472年)做的。
1701098553
1701098554
明代方以智在《物理小识》卷二《地类》中有段文字:
1701098555
1701098556
徐有贞张秋治水,或谓当浚一大沟,或谓多开支河。乃以一瓮窍方寸者一,又以一瓮窍方分者十,并实水发窍,窍十者先竭。
1701098557
1701098558
这里的瓮也即水箱。从文字上看,似乎并未明指两瓮开孔窍的面积相等。其实,按中国文化传统,比较事物的快慢、轻重、大小等问题时,必要以等距、等时或等积、等面为前提。《孟子·告子下》说:“金重于羽者,岂谓一钩金与一舆羽之谓哉?”方以智记述了徐有贞实验的前提条件:两瓮中一个开一大孔,以方寸为单位,设为1平方寸;另一个开十小孔,以方分为单位,则每个小孔面积当为:2分×5分或10分×1分。实验结果是,窍10个小孔的水箱先将水放完。
1701098559