1702632085
1702632086
知识普及 元分析
1702632087
1702632088
对一个重要问题只做一次实验,很难因此下结论。通常实验人员会做多次实验,它们的环境不同,设计不同,质量也不一样。我们能不能把不同实验的结果整合在一起,当作一个整体的结论呢?这就是“元分析”(meta-analysis)的概念。当然,各个实验之间的差异,使得我们无法直接把结果拼凑在一起。统计学家会用更加复杂的方法来整合结论,比如,元分析曾被用在二手烟的影响,以及补习是否可以提高美国学术能力评估测试的分数这些问题的研究中。
1702632089
1702632090
例8 低脂肪食品标签会导致肥胖症吗?
1702632091
1702632092
低脂肪食品标签对于食品消费的影响有多大?是否贴上低脂肪食品标签,人们就会吃掉更多的点心?答案可能取决于标签上是否有该食品是低脂肪食品以及关于食用量的信息。一项以大学员工、研究生和本科生作为实验对象的大型实验研究了这个问题。在十几个午后时段,所有实验对象都要在学校剧场里看60分钟电视节目,然后给节目打分。他们还被告知由于时间较晚,每个人会得到一瓶720毫升的冰水和一袋由受学生欢迎的校园餐厅Spice Box提供的格兰诺拉麦片,他们可以自己决定食用量。每名实验对象都拿到了一袋贴有3.25英寸×4英寸彩色标签的密封食品,上面注明这是一袋含有640卡路里热量(重量为160克)的格兰诺拉麦片。实验人员随机分配给实验对象的密封食品袋的不同之处在于,一种的标签上有“普通落基山格兰诺拉麦片”字样,另一种的标签上有“低脂肪落基山格兰诺拉麦片”字样。另外,有的标签上写着“内含一次食用量”、“内含两次食用量”,或者未注明食用量。当实验对象离开剧场时,他们被问及拿到的密封食品袋里的麦片是多大的食用量。在实验对象不在场的情况下,实验人员称了每一袋麦片的重量。实验对象的回答和称量结果是反应变量。
1702632093
1702632094
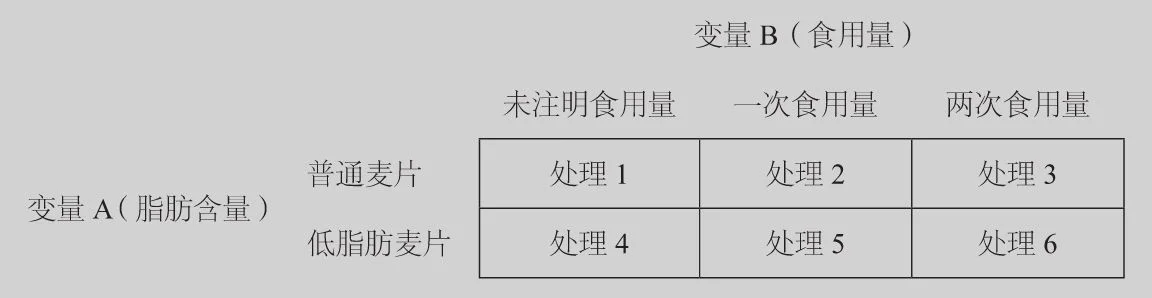
这个实验中有两个解释变量:脂肪含量,两种;食用量,3种。这可以组合成6种处理方式,见图6–1。
1702632095
1702632096

1702632097
1702632098
1702632099
图6–1 例8中的两个解释变量共组合出6种处理方式
1702632100
1702632101
练习
1702632102
1702632103
6.1 美味的蛋糕。一家食品公司准备推出一种什锦蛋糕,关键问题在于不能让蛋糕受到烘焙时间或温度变化的影响。在一个实验中,分别用148、160和171摄氏度将蛋糕烘焙1小时或1小时15分钟。用不同时间和不同温度的组合来制作蛋糕,每种处理方式对应10个蛋糕,由一组试吃者为每种蛋糕的口感和味道打分。
1702632104
1702632105
在这个实验中,解释变量和反应变量是什么?
1702632106
1702632107
画一个类似图6–1的图,展示该实验的处理方式。有多少种处理方式?需要制作多少个蛋糕?
1702632108
1702632109
实验人员经常希望能同时研究好几个变量的“联合效应”(combined effect)。几个因素的相互作用所产生的效应,无法根据每个因素的单独效应预测出来。长一点儿的广告也许会使观众对产品的兴趣增加,多播几次广告也许会使观众对产品的兴趣增加,但是如果我们既将广告加长,又多播几次,观众可能就会因厌烦而减少对产品的兴趣。例8的实验会帮我们找到答案。
1702632110
1702632111
配对设计与区块设计
1702632112
1702632113
完全随机化设计的实验是统计实验中最简单的一种,这类设计清楚地展示了控制与随机化这两项原则,不过,它往往比不上一些更复杂的设计。准确地说,用各种方式对实验对象做一些配对操作,得到的结果会比只进行随机化操作更精确。
1702632114
1702632115
兼具配对和随机化操作的常用设计就是“配对设计”(matched pairs design),配对设计只比较两种处理方式。先对实验对象进行配对操作,配对的两个实验对象在各方面应尽量相似。然后,利用抛硬币的方式,或者根据从表A中读取的随机数字为奇数或偶数来决定,把两种处理方式分别指派给配对的两个实验对象。有时候配对设计中的“一对实验对象”,实际上只包括一个实验对象,只是先后采取两种处理方式。此时,每个实验对象就是他/她自己的控制组。采取不同处理方式的顺序可能会影响实验对象的反应,所以会用抛硬币的方式来对每个实验对象采取不同处理方式的顺序进行随机化。
1702632116
1702632117
例9 可口可乐与百事可乐
1702632118
1702632119
百事可乐公司想要证明,可口可乐的爱好者在盲品两种可乐时,会更偏爱百事可乐。实验对象都是声称自己爱喝可口可乐的人,他们喝完两个未标示品牌的玻璃杯中的可乐之后,要说出更喜欢哪一杯。这就是配对设计:每个实验对象喝两种可乐,并做出比较。因为实验对象的反应和先喝哪种可乐有关,所以喝可乐的顺序应该随机化。
1702632120
1702632121
当超过一半的可口可乐爱好者在盲品后说百事可乐更好喝时,可口可乐公司声称该项实验有偏差。因为装百事可乐的玻璃杯上有M标记,而装可口可乐的玻璃杯上有Q标记。可口可乐公司说这意味着喜欢M这个字母的人超过喜欢字母Q的人。这个配对实验本身没有问题,但更严谨的做法是避免除两种可乐之外还存在其他差别。
1702632122
1702632123
这个配对设计的实验当中用到了比较处理方式和随机化两项原则。不过,此处的随机化并不是完全随机化,因为实验人员并没有将两种处理方式随机分配给所有实验对象,他们做的只是在每一个配对中随机化。这样的做法可经由配对减少实验对象间的差别所产生的影响。配对设计是“区块设计”(block design)的一个特例。
1702632124
1702632125
区块设计
1702632126
1702632127
一个区块(block)就是一组实验个体,这些个体在参加实验之前,被认为在某些方面的反应会很类似。在区块设计中,将个体随机分配到不同的组,对应不同的处理方式的这个步骤,是在每个区块里面分别进行的。
1702632128
1702632129
区块设计结合了用配对法来建立处理组的概念,以及用随机化方式产生各处理组的原则。区块是另一种形式的控制,通过把外部变量引入实验来组成区块,可以控制这些外部变量的影响。
1702632130
1702632131
例10 男性、女性和广告
1702632132
1702632133
男性和女性对广告的反应不一样。有一个实验比较了同一产品的三则电视广告的效果,除了人们对这三则广告的整体反应外,实验人员也想知道男性和女性的反应有何不同。
1702632134