1702635584
1702635585


1702635586
1702635587
1702635588
图14–4 38种汽车的油耗情况和重量的关系散点图
1702635589
1702635590
正相关与负相关
1702635591
1702635592
如果有两个变量,当其中一个变量的值高于平均数时,另一个变量的值也倾向于高于平均数,而当其中一个变量的值低于平均数时,另一个变量的值也倾向于低于平均数,则称这两个变量的关系是正相关的。此时,散点图是从左到右往上倾斜的。
1702635593
1702635594
如果有两个变量,当一个变量的值高于平均数时,另一个变量的值倾向于低于平均数,当前者低于平均数时,后者又倾向于高于平均数,则称这两个变量的关系是负相关的。此时,散点图是从左到右往下倾斜的。
1702635595
1702635596
每一幅散点图都有显著的形态。图14–2显示的是近似直线的趋势,图14–3显示的则是曲线关系(curved relationship),图14–4的曲线关系不是很明显。散点图的相关性强度,是由图中的点与某个明确的形态有多接近而决定的。图14–2和图14–3里的相关性不算强,与地球有相似距离的星系展示出的退行速度分布较分散,而人均GDP差不多的国家民众的预期寿命也可能很不一样。图14–4中的相关性较强。
1702635597
1702635598
例3 化石分类
1702635599
1702635600
始祖鸟是一种已灭绝的动物,有鸟类一样的羽毛,但也有牙齿和骨骼的长尾巴。目前,只发现了6个始祖鸟化石,由于这些化石的大小不一,科学家认为它们是属于不同的种类而非同一种类的个体。我们将测量其中5件有股骨(一种腿骨)和肱骨(一种上臂的骨头)的化石的骨头长度(单位是厘米),具体数据如下:
1702635601
1702635602


1702635603
1702635604
1702635605
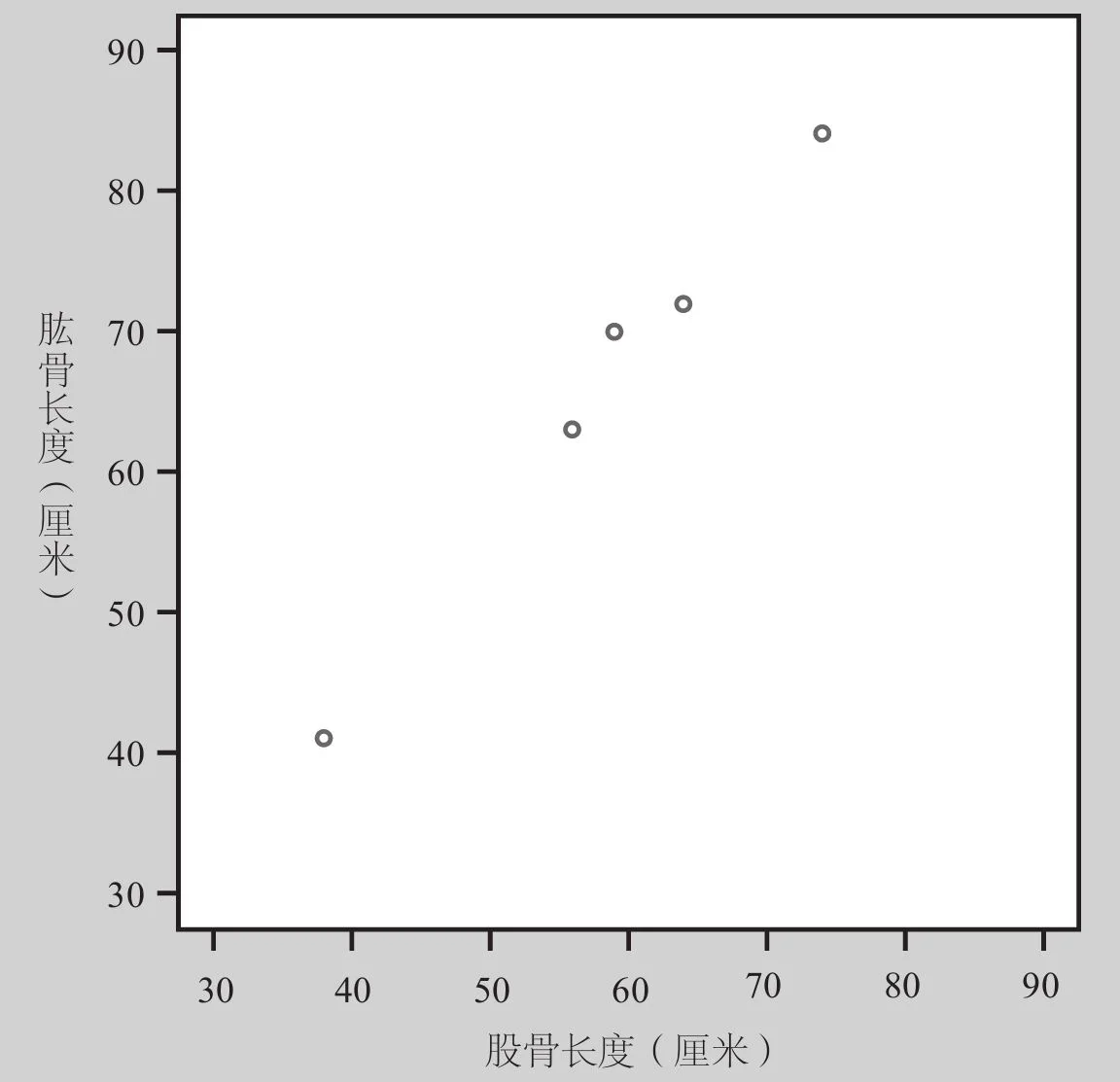
因为这两个变量之间并不存在解释变量和反应变量的区别,所以在散点图中把哪个标示在横轴上都没关系,如图14–5所示。
1702635606
1702635607
这个散点图显示出了很强的正线性相关关系。线性相关是重要的相关形式,因为它既常见,又简单易用。之所以说相关性很强,是因为点的分布十分接近一条直线。之所以说正相关,是因为当一种骨头的长度增加时,另一种骨头的长度也增加。从这些数据看,这5件化石应该属于同一种类的始祖鸟,大小不同是因为有的比较年幼。我们认为,在这两种骨头长度之间,不同种类应该有不同的相关性。因此,在这个散点图上,一个不同的种类应该会对应一个异常点。
1702635608
1702635609

1702635610
1702635611
1702635612
图14–5 5件始祖鸟化石的两种骨头(股骨与肱骨)长度的关系散点图
1702635613
1702635614
练习
1702635615
1702635616
14.2 脑容量和智力。几个世纪以来,人们一直在研究智力与脑容量的关系。最近一项研究用磁共振成像技术测量了一些人的脑容量。其中6个人的脑容量(单位为万像素)和IQ值如下:
1702635617
1702635618


1702635619
1702635620
1702635621
如果你还没试过,就用这些数据画一个散点图。其形式、方向和相关性强度如何?有无异常点?
1702635622
1702635623
相关系数
1702635624
1702635625
散点图可以呈现出两个变量之间相关关系的方向、形式和强度。当点的分布十分接近直线时,相关性就很强,而当点在直线附近很分散时,相关性就弱。光用眼睛看,不容易判断出相关性有多强。图14–6的两个散点图展示的是同一组数据,只是右边的图坐标涵盖范围较大,所以点变得比较靠近,似乎显示出较强的相关性。只要改一改散点图坐标轴上的刻度,或者点和点之间的空白处的大小,我们的眼睛就可能会上当。所以,我们得遵照数据分析的一般策略,除了图以外还要加上数值量度,“相关系数”(correlation)就是我们要用的量度。
1702635626
1702635627


1702635628
1702635629
1702635630
图14–6 同一组数据的两幅散点图。右图因为四周围空白较多,使得两个变量之间的相关性看上去比较强
1702635631
1702635632
相关系数
1702635633