1702639129


1702639130
图21-7的其他三条密度曲线分别展示了从总体中抽取2、10和25个样本的平均数的抽样分布。当样本量增大时,分布的形状变得更接近于正态分布了。平均数保持不变,标准差以μ/的比例减小。10个观察值的分布仍有点儿右偏,但已经接近于正态分布了;n=25的密度曲线更接近于正态分布。总体平均数的分布和10个、25个观察值的平均数分布相较,二者的区别很明显。
1702639131
1702639132


1702639133
1702639134
1702639135
图21-7 样本平均数的分布在样本量增大时会更接近于正态分布。单一观察值(n=1)的分布远非正态分布。2、10和25个观察值的平均数的分布越来越接近于正态分布
1702639136
1702639137
总体平均数的置信区间
1702639138
1702639139


1702639140


1702639141


1702639142


1702639143
的标准差同时取决于样本量n和标准差σ。我们知道n,但不知道σ。当n很大时,样本标准差s接近于σ,而且可以用s来估算σ,就像我们用样本平均数估算总体平均数μ一样。因此,估算标准差的公式就是s/。
1702639144
1702639145
现在,我们可以用计算p的置信区间的方法算出μ的置信区间。最重要的是,为了覆盖正态曲线下的中心区域C,我们必须从平均值开始向两侧各延伸z*个标准差的距离。从图21-5中可以看出C和z*之间的关系。
1702639146
1702639147
总体平均数的置信区间
1702639148
1702639149


1702639150
从一个平均数为μ的大型总体中抽出一个样本量为n的简单随机样本,这个样本的平均数是。当n足够大时,μ的近似置信度C的置信区间是:
1702639151
1702639152


1702639153
1702639154
1702639155
其中z*是置信度C的临界值(表21-1)。
1702639156
1702639157
我们在估算p时的提醒也适用于此,这个方法只在样本为简单随机样本且样本量n足够大时才有效。样本量多大才算足够大呢?答案取决于总体分布的真实形状。样本量n≥15通常足够大了,除非存在极端的异常值或明显的偏斜。对于明显偏斜的分布,样本量n≥40通常足够大了,如果没有异常值出现。
1702639158
1702639159


1702639160


1702639161


1702639162
当样本量n增加时,误差范围也以的比例减小。和s受异常值的影响很大,当出现异常值时,用和s做统计推断是存疑的,应该留意观察你的数据。
1702639163
1702639164
例7数学测试平均分
1702639165
1702639166
全美教育计划评估(NAEP)中包括一个对中学高年级学生的数学测试,分数范围为0~300。用毕达哥拉斯定理计算直角三角形的斜边长度,就是基础水平要求掌握的一个知识技能,高级水平要求掌握的知识技能之一是用三角函数计算三角形的边长。
1702639167
1702639168


1702639169
2009年,有51000名12年级学生作为NAEP的样本参加了数学测试。平均分=153,标准差s=34。假设这51000名学生是全体12年级学生的一个随机样本,基于这个样本,我们如何估计所有12年级学生的平均分μ?
1702639170
1702639171
μ的95%置信区间的计算,采用表21-1的临界值z*=1.96。这个置信区间是:
1702639172
1702639173
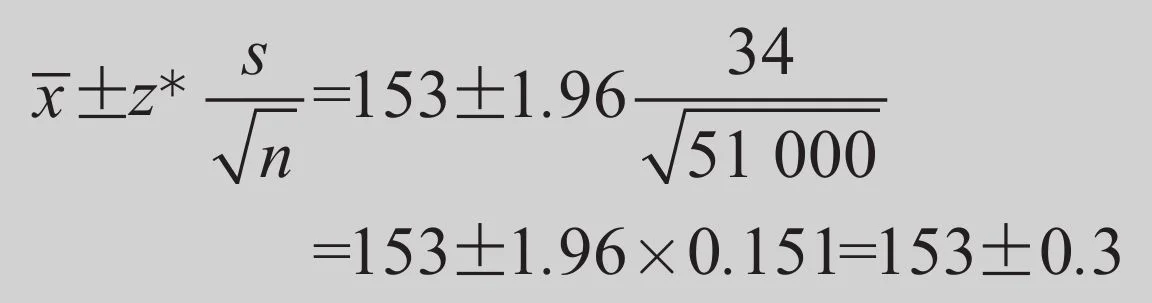
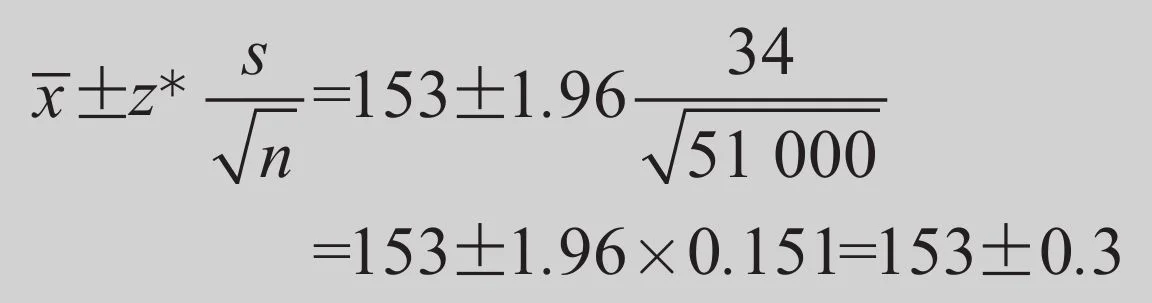
1702639174
1702639175
1702639176
我们有95%的把握认为,所有12年级学生的数学平均分在152.7到153.3之间。
1702639177
1702639178
练习