1702639611
1702639612
1702639613
这个数小于0.5。对于练习22.1,计算P值。这个结果在0.05的水平上具有统计学显著性吗?
1702639614
1702639615
检验总体平均数
1702639616
1702639617


1702639618


1702639619


1702639620
对总体平均数μ的统计检验的推理,遵循对总体比例p的推理步骤。最重要的思想是,如果零假设为真,则使用样本平均值的抽样分布来检验。根据你的数据计算,放入分布中,看看是否合理。在零假设为真时一个几乎不会出现的就是零假设不成立的证据。4个检验步骤也类似于对总体比例的检验过程。这里有两个例子,第一个是单边的,第二个是双边的。
1702639621
1702639622
例4 你会记账吗?
1702639623
1702639624


1702639625
在一个有关美国劳动者教育水平的讨论中,一位悲观主义者说道:“年轻人都不会记账。”全美成年人文化水平评估(NAAL)所做的调查表明,如果在其量化测试中获得290或更高分数,就表明实验对象具有记账之类的技能。NAAL测试过一个包含2168名年轻男性(19~24岁)的样本,他们的平均分=276,比会记账所要求的分数低。这个样本结果是所有年轻男性的NAAL测试分数低于290分的一个好的证据吗?这个样本的测试分数标准差s=112。
1702639626
1702639627
假设。悲观主义者声称NAAL测试的平均分低于290,这是备择假设,我们要找到支持它的证据。假设为:
1702639628
1702639629
H0:μ=290
1702639630
1702639631
Ha:μ>290
1702639632
1702639633


1702639634


1702639635
抽样分布。如果零假设为真,样本平均数大致一个平均数μ=290,标准差的正态分布。我们用样本标准差s代替未知的总体标准差σ。
1702639636
1702639637


1702639638
数据。NAAL的样本给出了=276,所以标准分是:
1702639639
1702639640


1702639641
1702639642
1702639643
也就是说,样本的结果距离平均分约5.83个标准差,一般而言,达到平均分的年轻人才具备记账的技能。
1702639644
1702639645
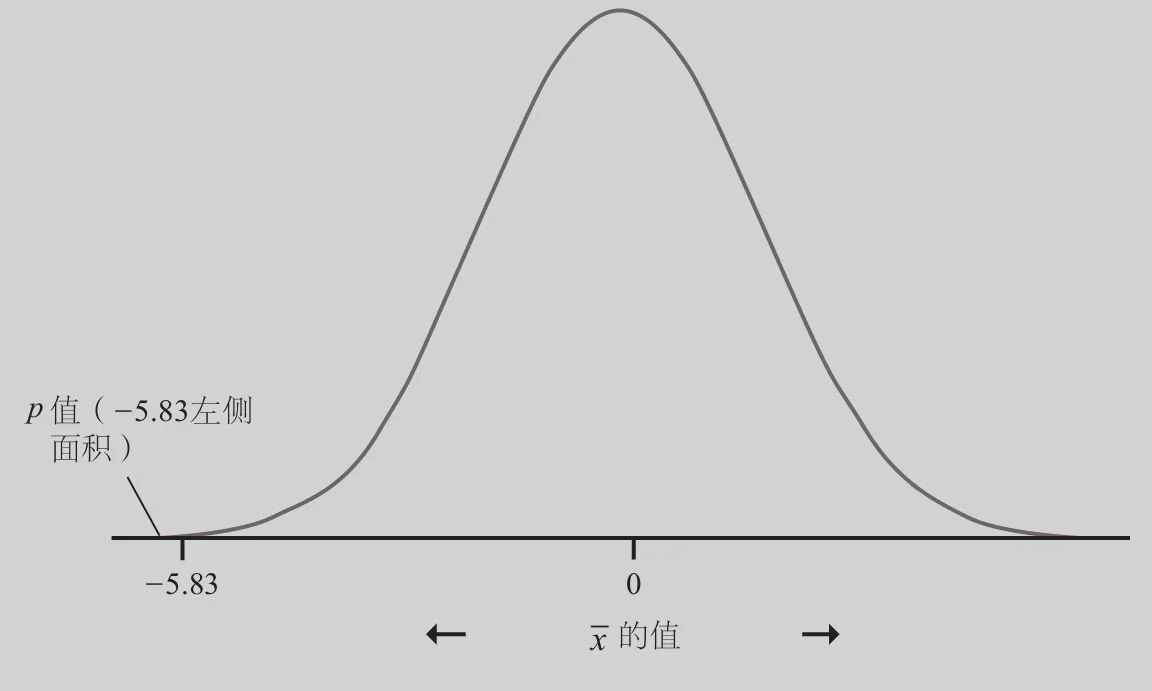
P值。图22-4在正态分布曲线上标示了样本结果-5.83(以标准差为单位刻度),该正态分布曲线代表零假设为真时的抽样分布。由于我们使用的是标准差,因此这条曲线的平均数为0,标准差为1。我们单边检验的P值是该正态分布曲线上-5.83左侧的面积,图22-4显示这个面积非常小。表B的最小值是-3.4,从表B中看到-3.4就是第0.03百分位数,所以其左侧面积是0.0003。由于-5.83比-3.4小,所以我们知道其左侧面积要比0.0003还小。所以,我们的P值小于0.0003。
1702639646
1702639647

1702639648
1702639649
1702639650
图22-4 样本平均数的标准分是-5.83时的单边检验的P值
1702639651
1702639652
结论。小于0.0003的P值是一个很有说服力的证据,证明年轻人(19~24岁)的平均分低于记账所要求的知识水平。
1702639653
1702639654
知识普及 抓住作弊者
1702639655
1702639656
很多学生都参加过有许多道选择题的考试。为试卷打分的计算机是否可以筛选出那些答案看上去很类似的试卷呢?聪明的人类已经创造了一种方法,不仅能看答案是否一样,而且会看相同答案的普遍程度,以及相似试卷的总分数。这个方法接近于正态分布,计算机能用这种方法把超出±4个标准差的类似试卷筛选出来。
1702639657
1702639658
例5 经理人的收缩压
1702639659
1702639660

