1702906877


1702906878


1702906879


1702906880
(2),每当
1702906881
1702906882


1702906883


1702906884


1702906885
(3),每当
1702906886
1702906887


1702906888


1702906889
(4)在给定先验信念满足贝叶斯法则,也就是,就有
1702906890
1702906891


1702906892
1702906893
1702906894


1702906895


1702906896


1702906897


1702906898
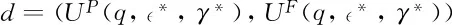
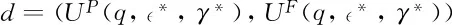
1702906899
一项均衡具有四个特征。首先,行政机构和外国政府在约束条件下(正如之前情况)在条约集合内提出供批准的点,同时也是双方条约谈判的纳什谈判解。对任意均衡(),我们重新界定集合;和不同意点。这样再次设定了一个谈判问题。第二,背书人只会在协定最优条件下具有可能支持协定。第三,选择者只会在给定信念条件下这些条约为最优情况下批准条约。第四,信念同贝叶斯法则和所传递的信息一致。
1702906900
1702906901
需要注意之前的μ不是源于之前的Ξ,而是Ψ。请注意C并不知道f的相对地位。但是,C了解p,也清楚f在支持区间[-1,1]内独立地源自Ξ,而且一旦选定,P和F会在可批准的条约集合内谈判纳什解。那么,什么构成了C对提出的协定的先验信念?我们通过P和F从协定集合中选择NBS的常识,把对提出的协定的这些信念的简化模式视为分配性函数Ψ,Ψ来自Ξ;也就是Ψ(a′)代表了选择者之前的信念:P和F已谈判达成一项政策a′或者小于概率Ψ(a′)的政策。这是我们把信念结构从类型变成协定的方式,也是把偏好转化为政策的方式。这一简化模型的密度记为ψ。但是回想纳什谈判解取决于预期:P和F在谈判时已然知道他们的提案要接受背书人的检验,而且像立法机构的选择者会根据这些背书来最优选择。因此,Ψ是在作出背书之前关于协定的信念陈述。但是在谈判已经开始之后,它就不再是先验信念的陈述,也不是后验信念。然后,这些信念确实在定义序贯均衡上发挥作用,也是因为这个原因,我们可以将其称为暂时信念(interim beliefs)。
1702906902
1702906903
盲目接受的结果
1702906904
1702906905
当博弈是不完全信息的,并且没有背书者,均衡结果如下:
1702906906
1702906907
命题A1.2:在不完全信息且没有背书者的情况下,多个议程设定者的国内博弈的均衡是
1702906908
1702906909


1702906910
1702906911
1702906912
证明:请参考Cameron and Jung(1992),命题2。
1702906913
1702906914


1702906915


1702906916


1702906917


1702906918
现在再回到有背书者的博弈,我们只考察这样的均衡:只要有更好的非混同均衡策略存在,背书者就不会运用混同均衡(Banks 1990,1991)。按照卡梅伦和荣格(Cameron and Jung 1992)的文章,如果在均衡状态下,背书者将采取混同策略。如果背书者采取混同策略,且其中使用的所有信息都是正概率的(positive probability),那么策略是毫无意义的。如果战略不是混同的,那么我们可以说背书者愿意发出信息。如果背书者愿意发出信息,而且当且时,背书者在均衡下发出有用信息;也就是只有当信息改变了背书者行为时,信息才是有用的。混同均衡在无成本的信号博弈中总是存在的,我们感兴趣的是被传递的信息如何影响国际条约的性质。
1702906919
1702906920
我们将注意力集中于这样的均衡:信息0(1)具有支持现状Q(或者条约草案a)的实质含义。而且,卡梅伦和荣格(Cameron and Jung 1992)表明这些混同均衡并不能经得起“新语证明”精炼(“neologism proof”refinement)均衡检验。在均衡中如果背书者观测到a则发送信息1,观测到a′则发送0,那么就存在“镜像”均衡(mirror-image equilibrium),其中观测和信号是相反的。我们简单地将这些均衡排除,因为它们没有有意义的解释。这样我们就得到了满足这些条件的所有可能的纯策略均衡。
1702906921
1702906922


1702906923


1702906924
辅助定理A1.2:在任何均衡下,(1;0)。
1702906925
1702906926
证明:请参见Cameron and Jung 1992。