1702906911
1702906912
证明:请参考Cameron and Jung(1992),命题2。
1702906913
1702906914


1702906915


1702906916


1702906917


1702906918
现在再回到有背书者的博弈,我们只考察这样的均衡:只要有更好的非混同均衡策略存在,背书者就不会运用混同均衡(Banks 1990,1991)。按照卡梅伦和荣格(Cameron and Jung 1992)的文章,如果在均衡状态下,背书者将采取混同策略。如果背书者采取混同策略,且其中使用的所有信息都是正概率的(positive probability),那么策略是毫无意义的。如果战略不是混同的,那么我们可以说背书者愿意发出信息。如果背书者愿意发出信息,而且当且时,背书者在均衡下发出有用信息;也就是只有当信息改变了背书者行为时,信息才是有用的。混同均衡在无成本的信号博弈中总是存在的,我们感兴趣的是被传递的信息如何影响国际条约的性质。
1702906919
1702906920
我们将注意力集中于这样的均衡:信息0(1)具有支持现状Q(或者条约草案a)的实质含义。而且,卡梅伦和荣格(Cameron and Jung 1992)表明这些混同均衡并不能经得起“新语证明”精炼(“neologism proof”refinement)均衡检验。在均衡中如果背书者观测到a则发送信息1,观测到a′则发送0,那么就存在“镜像”均衡(mirror-image equilibrium),其中观测和信号是相反的。我们简单地将这些均衡排除,因为它们没有有意义的解释。这样我们就得到了满足这些条件的所有可能的纯策略均衡。
1702906921
1702906922


1702906923


1702906924
辅助定理A1.2:在任何均衡下,(1;0)。
1702906925
1702906926
证明:请参见Cameron and Jung 1992。
1702906927
1702906928
对提案的任何背书都不会降低该条约草案被批准的概率。重要的是,如果选择者听从背书者的意见,背书者将作出诚实的背书(比如,背书者真的希望维持现状的提案)。这是因为背书者从来不会作出关于接受或者拒绝协定草案的最终选择。我们现在定义三组战略:背书者均衡(endersement equilibrium)、对抗均衡(recalcitrant equilibrium)以及顺化均衡(accommodating equilibrium)。定义E的偏好集合为
1702906929
1702906930
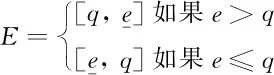
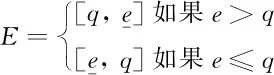
1702906931
1702906932
1702906933
定义:下列战略集合将被称作批准均衡
1702906934
1702906935


1702906936
1702906937
1702906938
在背书均衡中,如果aT处于q和e之间,提案者同意提供aT。如果aT不在其间,P和F在制约条件下会提出最接近可批准的条约——或是q或者是e。当背书者了解到提出的方案处于自己偏好政策集合中(相对于维持现状),背书者会积极地发出信号,而选择者C会倾听E的解释,并依赖背书信息来作出批准决定。
1702906939
1702906940
定义:下面的战略集合称为对抗均衡
1702906941
1702906942


1702906943
1702906944
1702906945
P和F将同意提出没有受到制约的方案aT,如果相对于现状政策,aT处于背书者的偏好政策集合中,背书者将背书。国会将抵制,不会批准任何协定。
1702906946
1702906947
定义:下面的战略集合称为顺化均衡
1702906948
1702906949


1702906950
1702906951
1702906952
P和F再次达成协定提出非受约束的方案aT,期待该方案能够被接受。背书者再次诚实地作出反应,因为选择者的信念是乐观的,它会接受任何提案。下面的命题具体化了这些均衡存在的条件,并且当q<max{e,c},证明了这些情况。当q>max{e,c},其条件在括号内具体表示,这些结果适用于相对的情况。当q∈(e,c)或q∈(c,e),命题A1.4适用。
1702906953
1702906954
命题A1.3:我们考虑q<e<c(或c<e<q)的情况,将θ定义为在T上的点,因此
1702906955
1702906956


1702906957
1702906958
1702906959


1702906960

