1703389402
100c(损耗)+500c+500v+500m=1600每年周转10次,全部年产品就是:
1703389403
1703389404
1000c(损耗)+5000c+5000v+5000m=16000,
1703389405
1703389406


1703389407
C=11000,m=5000,
1703389408
1703389409
我们现在假定有资本Ⅱ:其中固定资本9000,每年的损耗1000,流动不变资本1000,可变资本1000,剩余价值率100%,可变资本每年周转5次。因此,可变资本每个周转期间的产品将是:
1703389410
1703389411
200c(损耗)+1000c+1000v+1000m=3200,周转5次,全部年产品就是:
1703389412
1703389413
1000c(损耗)+5000c+5000v+5000m=16000,
1703389414
1703389415


1703389416
C=11000,m=5000,
1703389417
1703389418
我们再假定有资本Ⅲ,其中完全没有固定资本,只有流动不变资本6000和可变资本5000。剩余价值率100%,每年周转一次。这时,一年的全部产品就是:
1703389419
1703389420
6000c+5000v+5000m=16000,
1703389421
1703389422
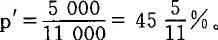
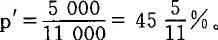
1703389423
C=11000,m=5000,
1703389424
1703389425


1703389426
因此,在所有这三个场合,我们有相同的年剩余价值量=5000;并且,因为所有这三个场合的总资本相同,即=11000,所以也有相同的利润率
1703389427
1703389428
但是,如果上述资本Ⅰ的可变部分不是每年周转10次,而是每年只周转5次,情况就不同了。这时,周转一次得到的产品就是:
1703389429
1703389430
200c(损耗)+500c+500v+500m=1700。
1703389431
1703389432
或年产品是:
1703389433
1703389434
1000c(损耗)+2500c+2500v+2500m=8500,
1703389435
1703389436


1703389437
C=11000,m=2500,
1703389438
1703389439
利润率下降了一半,因为周转时间延长了一倍。
1703389440
1703389441
因此,一年内占有的剩余价值量,等于可变资本一个周转期间所占有的剩余价值量乘以一年内可变资本周转的次数。如果我们把一年内占有的剩余价值或利润叫作M,一个周转期间所占有的剩余价值叫作m,一年内可变资本周转的次数叫作n,那么,M=mn,年剩余价值率M′=m′n。这一点已经在第二册第十六章第一节说明过了。
1703389442
1703389443


1703389444


1703389445


1703389446


1703389447


1703389448


1703389449
不言而喻,利润率的公式p′=只有在分子中的v和分母中的v是同一个东西的时候,才是正确的。在分母中,v是总资本中平均作为可变资本用于工资的整个部分。在分子中,v首先只是由下面的事实规定的:它曾经生产并占有一定量的剩余价值m;而剩余价值和v的比率,就是剩余价值率m′。只是通过这样的途径,p′=这个方程式才转化为另一个方程式p′=m′现在,分子中的v要进一步加以规定:它必须和分母中的v,也就是和资本C中的整个可变部分相等。换句话说,p′=这个方程式,只有在m是指可变资本的一个周转期间所生产的剩余价值的时候,才能够转化为另一个方程式p′=而不致发生错误。如果m只包括这个剩余价值的一部分,那么m=m′v固然还是正确的,但这个v在这里,就比C=c+v中的v小,因为它比投在工资上的全部可变资本小。但是,如果m比v周转一次得到的剩余价值大,那么这个v的一部分,甚至它的全部,就曾经两次执行职能,先是在第一次周转中,然后又在第二次周转中,或者,在第二次以及以后各次周转中执行职能;所以,生产剩余价值并代表所付工资总额的v,就比c+v中的v大,因此计算也就不正确了。
1703389450
1703389451

