1703536363
这个领域的论文都在寻求如何参数化一组随机变量的协方差矩阵,这种方法以一组可观测的状态变量为条件并且普遍采用的是因变量过去的过滤值。设向量y是一组类似资产收益率的随机变量,那么目标是参数化和估计。
1703536364
1703536365
Ht=Vt-1(yt) (3-1)
1703536366
1703536367
从这个条件协方差的估计中可以立即得到条件相关系数和条件方差。变量i和j间的条件相关系数的标准定义是
1703536368
1703536369


1703536370
1703536371
1703536372
如果用矩阵来表示,条件相关矩阵和方差矩阵为
1703536373
1703536374


1703536375
1703536376
1703536377
这里符号diag[A]代表一个具有与A同样的对角元素但其他元素为0的矩阵。这些表达式意味着我们熟悉的一个协方差矩阵表达式
1703536378
1703536379
Ht=DtRtDt (3-4)
1703536380
1703536381
如果随机变量间不存在线性相关,那么H和R都是正定矩阵。对这个动态问题的参数化应该要确保所有协方差矩阵和相关矩阵是正定的,这样就确保所有的波动为正。由于这些矩阵实际上是随机过程,所以只要求它们正定的概率是1。也就是说,对于所有过去具有正定概率的历史记录,协方差矩阵应该是正定的。如果情况不是这样,那么会存在y的线性组合,并且明显具有0和负的方差。一个权重为w的投资组合的条件方差为
1703536382
1703536383


1703536384
1703536385
1703536386
如果H是正定的,那么上式是正的。如果H只是半正定的,那么会出现0方差的投资组合;如果H是不定矩阵,那么会出现负方差的投资组合。在资产配置问题或风险管理问题中,投资组合被最优化来降低风险。巧妙的计算会找到这些明显无风险或者负风险的投资组合并且向它们投资。但是,为了保证这些应用的成功,排除这种可能性是至关重要的。一般来讲,负或0方差的投资组合必须被认为是对协方差矩阵的一个误设。
1703536387
1703536388
1703536389
1703536390
1703536391
预见相关性:风险管理新范例 [:1703535707]
1703536392
预见相关性:风险管理新范例 3.1 移动平均法和指数平滑法
1703536393
1703536394
最广泛使用的协方差估计量是最简单的。这些估计量对待协方差矩阵的每个元素同样并且经常假定均值为0。这些模型是移动平均波动和相关,通常称为历史波动和相关。
1703536395
1703536396


1703536397
1703536398
1703536399
指数平滑法已经被风险计量学(RiskMetrics)用来计算风险。对于所有的i,j,它定义为
1703536400
1703536401


1703536402
1703536403
1703536404
这两个模型中,t时刻的观测值的协方差矩阵都基于t-1时刻的信息。在两种情况下,都有唯一一个支配整个协方差矩阵估计量的参数,在移动平均模型中这个参数是m,在指数平滑法中是λ。
1703536405
1703536406
这些协方差估计量在弱的假设条件下是正定的。在矩阵表达式中,这些条件更容易看到。设yt是n×1资产收益向量,那么这些估计量可以写成
1703536407
1703536408
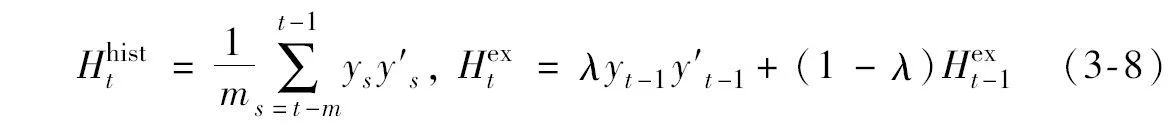
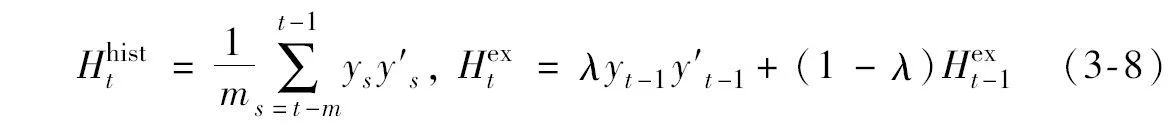
1703536409
1703536410
1703536411
由于每个估计量是半正定矩阵的平均或者加权平均,所以估计量至少是半正定的。如果最开始的H1是正定矩阵,那么指数平滑估计量将是正定的,但一般来讲,正定性对ys的假设要求非常弱,比如要求它们有一个非奇异的协方差矩阵并且只是弱相关。当然,历史协方差矩阵不可能是正定的,除非m>n。
1703536412