1703624540
采用同Van Breukelen法以及Wagner和Tito法类似的概念,Campisi(2000)提出将固定收益投资组合的收益率分解为利息收入和价格收益,具体如图7-4所示。
1703624541
1703624542
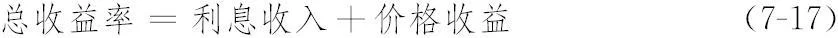
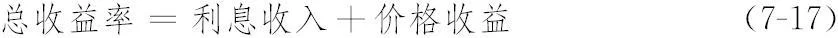
1703624543
1703624544
1703624545
式中
1703624546
1703624547


1703624548
1703624549
1703624550


1703624551
1703624552
1703624553
图7-4 Campisi框架
1703624554
1703624555
国债影响表示国债收益率变化的影响。投资组合对收益率变化的敏感度由修正久期表示,具体参考式(4-106)。
1703624556
1703624557
实际上,Campisi将式(7-1)中本币利率替换为利息收入,同时包括了利差变化影响。
1703624558
1703624559


1703624560
1703624561
1703624562
式中 Ii ——类别i的利息收入;
1703624563
1703624564
Di ——类别i的修正久期;
1703624565
1703624566
Δyi ——久期Di 的国债收益率变化;
1703624567
1703624568
Δysi ——类别i的参考基准利差变化;
1703624569
1703624570
εi ——无法被利息收入、国债和利差影响解释的剩余部分。
1703624571
1703624572
同样,参考基准收益率如下计算:
1703624573
1703624574


1703624575
1703624576
1703624577
式中 Ibi ——类别i的参考基准利息收入;
1703624578
1703624579
Dbi ——类别i的参考基准修正久期。
1703624580
1703624581
显然,对于参考基准收益率的分解应该不包括剩余部分,任何没有被利息收入和国债影响解释的部分都应该归于利差影响。
1703624582
1703624583
我们对表7-15中数据采用Campisi框架进行了归因分析计算。
1703624584
1703624585
表7-15 Campisi框架
1703624586
1703624587


1703624588
1703624589