1703624977
1703624978


1703624979
1703624980
1703624981
相互作用:
1703624982
1703624983


1703624984
1703624985
1703624986
Davies和Laker方法建立了资产配置、股票选择和相互作用的总贡献的计算方法。他们2001年的论文并没有提及每个类别的收益率如何计算,但他们暗示使用Carino方式的算法来计算每个类别的贡献,然后再将每个类别的贡献相加。
1703624987
1703624988
再次使用表8-1中的数据,我们计算了每个季度的Brinson名义基金收益率并将其复利化,具体如表8-14所示。
1703624989
1703624990
表8-14 Brinson名义基金收益率
1703624991
1703624992


1703624993
1703624994
1703624995
在表8-15中计算了整个时段的总或“精确”归因影响。
1703624996
1703624997
表8-15 精确归因影响
1703624998
1703624999


1703625000
1703625001
1703625002
总体水平的归因影响只可以采用这种方法计算。为了计算每个类别的贡献,我们必须对每个影响采用平滑算法。
1703625003
1703625004
这种方法合并了算术法和几何法的概念,是算术法和完全几何法之间的一个进化阶段。
1703625005
1703625006
Davies和Laker方法也复利化了Brinson模型的缺点(即相互作用),这使得结果更加没有意义。所以更明智的是将相互作用同股票选择影响合并起来,将股票选择定义为:
1703625007
1703625008


1703625009
1703625010
1703625011
所以股票选择和资产配置完全解释了超额收益率。
1703625012
1703625013


1703625014
1703625015
1703625016
多时段几何归因分析
1703625017
1703625018
多时段几何法归因分析并没有算术法多时段归因的链接问题。第3章展示了几何法超额收益率随着时间推移可以进行复利化。几何法归因分析也可以复利化以提供单一时段的超额收益率。所以将式(5-31)代入式(3-26):
1703625019
1703625020


1703625021
1703625022
1703625023
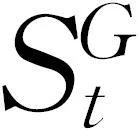
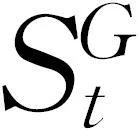
1703625024
式中 ——时段t的总几何法股票选择影响;
1703625025
1703625026

